All AP Physics C: Mechanics Resources
Example Questions
Example Question #1 : Magnetism
A proton traveling 


To calculate the magnetic force of a single charge, we use 



Since this magnetic force causes the proton to travel in a circular path, we set this magnetic force equation equal to the centripetal force equation.



Using the values given in the question, we can solve for the radius.
Example Question #1 : Magnetism
Which of the following best describes the net magnetic flux through a closed sphere, in the presence of a magnet?
Positive only if the north pole of the magnet is within the surface
More than one of the other options is true
Zero regardless of the orientation of the magnet
Negative only if the north pole of the magnet is within the surface
Zero only if the magnet is completely enclosed within the surface
Zero regardless of the orientation of the magnet
The net magnetic flux (or net field flowing in and out) through any closed surface must always be zero. This is because magnetic field lines have no starting or ending points, so any field line going into the surface must also come out. In other words, "there are no magnetic monopoles."
Example Question #1 : Magnetism
A particle of charge 



Relevant equations:
Set the magnetic force equal to the centripetal force, since the magnetic force is directed towards the center of the particle's circular path and centripetal force is defined as the net force towards the center of a circular path.
Rearrange to isolate the velocity:
Determine the distance, 

Plug this distance and velocity into 

Example Question #1 : Magnetism
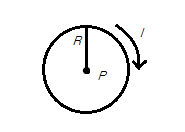
Consider a current-carrying loop with current 


A particle with charge 

The correct answer is zero. To calculate the force of a magnetic field on a moving charged particle, we use the cross product. We know that if the magnetic field is parallel to the velocity vector of the particle, then the force produced is zero.
Because our magnetic field in this case is going in the same direction as the velocity of the particle, we know that the magnetic force on the particle is zero.
Example Question #1 : Magnetism
Consider two long, straight, current-carrying wires at distance 

If the two wires described are not held in place, what motion will result from the magnetic fields produced?
The wires will move away from each other
The wires will rotate counterclockwise
The wires will remain in place
The wires will rotate clockwise
The wires will move toward each other
The wires will move away from each other
The answer is that the wires will move from each other. Using our right hand rule, we know that the magnetic fields produced by each wire are in the same direction, as long as their currents oppose. Using the right hand rule again to determine the direction of the force exerted on each wire by the magnetic field with which they are interacting yields a force in the direction away from the other wire for each wire.
Example Question #1 : Understanding Magnetic Fields And Wires
Two infinitely long wires having currents 



The current 



What is the magnitude and direction of the net magnetic field at the point 
At point 

At point 

The addition of these two vectors, both pointing in the same direction, results in a net magnetic field vector of magnitude 
Example Question #191 : Ap Physics C

Consider a current-carrying loop with current 
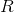

What is the direction of the magnetic field produced?
Clockwise
Out of the screen
Into the screen
Counterclockwise
There is no resultant magnetic field
Into the screen
The correct answer is into the page. As the current is moving clockwise, we can use our right hand rule for magnetic fields produced by a current-carrying loop. Curl the fingers of your right hand in the direction of the current. This should result in your thumb pointing toward the screen, indicating the direction of the magnetic field.
Example Question #191 : Ap Physics C

Consider a current-carrying loop with current 


What would happen to the magnetic field at point 
The new magnetic field would be four times as strong as the original
The new magnetic field would be eight times as strong as the original
The new magnetic field would be four times weaker than the original
The new magnetic field would reverse direction
The new magnetic field would be eight times weaker than the original
The new magnetic field would be eight times as strong as the original
The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:
Using out altered values, we can derive a ratio to determine the change in magnetic field.
The resulting field will be eight times stronger than the original.
Example Question #1 : Understanding Magnetic Fields And Wires

Consider a current-carrying loop with current 


What is the magnitude of the magnetic field at point 
There is no magnetic field at point
The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:
Example Question #2 : Magnetism
Consider two long, straight, current-carrying wires at distance 

What is the magnitude of the magnetic field at a point equidistant from both wires?
Zero
Using our right hand rule for magnetic fields produced by current-carrying wires, we know that the magnetic field produced by each wire is in the same direction within the distance between the wires. Therefore, we know that the total magnetic field is simply the magnetic field of one of the wires multiplied by two.
Use the equation for magnetic field:
Multiply by two, since the magnetic field will be equal for each wire, and substitute the given variables:
All AP Physics C: Mechanics Resources