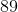All Basic Arithmetic Resources
Example Questions
Example Question #1 : Basic Statistics
For her calculus class, Marie has scored 



To find the average of a set of numbers, add up the individual values and divide by the total number of values you have.
For the test scores, we can set up the following equation with x being the score on the fourth test:
Now, solve for x
Example Question #2 : Basic Statistics
Find the mean of the following set of numbers:
To find the mean of a set of numbers, you must add them all and then divide their sum by the number of total members of the set.




giving us a mean of 
Example Question #3 : Basic Statistics
Jimmy's dog had 6 puppies. He weighed the puppies right after they were born. Their weights were 657 grams, 789 grams, 456 grams, 554 grams, 635 grams, and 446 grams. In grams, what was the mean weight of the puppies?
The mean of a set of numbers is the same as its average.
So then, to find the mean weight for the puppies,
Example Question #4 : Basic Statistics
Danielle tracked how much she paid per meal for the past five meals. She paid 
To find the average (also known as the mean), we use the following formula:
So, for the numbers that are given in the question, we can set up this equation:
Example Question #5 : Basic Statistics
Judy received these scores on her last four math tests:



Her teacher calculates the final grade from the mean of five tests, which are all weighted equally. If Judy gets a 
To find Judy's overall grade, you must find the mean of all five test scores.
Add together all five scores:
Then divide the sum by the total number of scores:

Example Question #1 : Statistics And Probability
What is the mean of 44, 22, 134, and 200?
66
144
88
100
100
To find the mean, you must add all of the numbers together and divide by the amount of numbers. In this case there are four numbers so, we must deivide the total sum by 4.
Example Question #2 : Statistics And Probability
Calculate the mean of the following numbers: 11, 13, 16, 13, 14, 19, 13, 13
First, calculate the sum of all of the numbers.
Next, divide by the total number.
Example Question #3 : Statistics And Probability
The class average in a class of 15 is 86%. If one additional student earns a 100% in the class, what is the new class average.
There is not enough information to answer this question
None of the available answers
We can treat this as if the entire class had exactly 86% as their average, so the new average is:
Example Question #1 : How To Find Mean
What is the mean of the following numbers?
88,99,31,47,68,27
To find the mean you add all of the numbers together and divide it by the amount of numbers. In this case there are six numbers so
The answer is 
Example Question #1 : Basic Statistics
The mean of the set 

To find mean, we add up the values in a set and divide by the number of terms in that set. We begin this problem with the knowledge that the mean of the first set is 20. Since that set contains five numbers, we know that its total sum must be 100 (since 100 divided by 5 is 20).
so 
Now, the only step left is to find the mean of 
These values add up to 125, and when we divide by 5, we are left with a final answer of 25.
Certified Tutor
Certified Tutor
All Basic Arithmetic Resources