All Basic Geometry Resources
Example Questions
Example Question #1 : How To Find An Angle Of A Line

Examine the diagram. Which of these conditions does not prove that 
Any of these statements can be used to prove that 


If 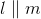
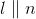

If 


If 


However, 


Example Question #2 : How To Find An Angle Of A Line
An isosceles triangle has an interior angle that measures 
This triangle cannot exist.
By the Isosceles Triangle Theorem, two interior angles must be congruent. However, since a triangle cannot have two obtuse interior angles, the two missing angles must be the ones that are congruent. Since the total angle measure of a triangle is 

Example Question #1551 : Basic Geometry
Straight
Scalene
Obtuse
Right
Acute
Obtuse
Obtuse angles are greater than 
Scalene is a designation for triangles that have one angle greater than 
Acute angles are less than 


Therefore this angle is obtuse.
Example Question #4 : How To Find An Angle Of A Line
When two parallel lines are crossed by a third line (called the transversal), the measure of the angles follows a specific pattern. The pairs of angles inside the two lines and on opposite sides are called alternate interior angles. Alternate interior angles, such as 



Example Question #4 : How To Find An Angle Of A Line
Mark is training for cross country and comes across a new hill to run on. After Mark runs 


The same as the angle of inclination
Cannot be determined
Upon reading the question, we're left with this spatial image of Mark in our heads. After adding in the given information, the image becomes more like
The hill Mark is running on can be seen in terms of a right triangle. This problem quickly becomes one that is asking for a mystery angle given that the two legs of the triangle are given. In order to solve for the angle of depression, we have to call upon the principles of the tangent function. Tan, Sin, or Cos are normally used when there is an angle present and the goal is to calculate one of the sides of the triangle. In this case, the circumstances are reversed.
Remember back to "SOH CAH TOA." In this problem, no information is given about the hypotenuse and nor are we trying to calculate the hypotenuse. Therefore, we are left with "TOA." If we were to check, this would work out because the angle at Mark's feet has the information for the opposite side and adjacent side.
Because there's no angle given, we must use the principles behind the tan function while using a fraction composed of the given sides. This problem will be solved using arctan (sometimes denoted as 
Example Question #1 : Geometry
Two angles are supplementary and have a ratio of 1:4. What is the size of the smaller angle?
Since the angles are supplementary, their sum is 180 degrees. Because they are in a ratio of 1:4, the following expression could be written:
Example Question #2 : Geometry

AB and CD are two parrellel lines intersected by line EF. If the measure of angle 1 is 
The angles are equal. When two parallel lines are intersected by a transversal, the corresponding angles have the same measure.
Example Question #5 : How To Find An Angle Of A Line
Lines A and B in the diagram below are parallel. The triangle at the bottom of the figure is an isosceles triangle.
What is the degree measure of angle 
Since A and B are parallel, and the triangle is isosceles, we can use the supplementary rule for the two angles, 








Example Question #1 : Geometry
Figure not drawn to scale.
In the figure above, APB forms a straight line. If the measure of angle APC is eighty-one degrees larger than the measure of angle DPB, and the measures of angles CPD and DPB are equal, then what is the measure, in degrees, of angle CPB?
114
33
40
50
66
66
Let x equal the measure of angle DPB. Because the measure of angle APC is eighty-one degrees larger than the measure of DPB, we can represent this angle's measure as x + 81. Also, because the measure of angle CPD is equal to the measure of angle DPB, we can represent the measure of CPD as x.
Since APB is a straight line, the sum of the measures of angles DPB, APC, and CPD must all equal 180; therefore, we can write the following equation to find x:
x + (x + 81) + x = 180
Simplify by collecting the x terms.
3x + 81 = 180
Subtract 81 from both sides.
3x = 99
Divide by 3.
x = 33.
This means that the measures of angles DPB and CPD are both equal to 33 degrees. The original question asks us to find the measure of angle CPB, which is equal to the sum of the measures of angles DPB and CPD.
measure of CPB = 33 + 33 = 66.
The answer is 66.
Example Question #1 : Geometry
One-half of the measure of the supplement of angle ABC is equal to the twice the measure of angle ABC. What is the measure, in degrees, of the complement of angle ABC?
54
18
36
90
72
54
Let x equal the measure of angle ABC, let y equal the measure of the supplement of angle ABC, and let z equal the measure of the complement of angle ABC.
Because x and y are supplements, the sum of their measures must equal 180. In other words, x + y = 180.
We are told that one-half of the measure of the supplement is equal to twice the measure of ABC. We could write this equation as follows:
(1/2)y = 2x.
Because x + y = 180, we can solve for y in terms of x by subtracting x from both sides. In other words, y = 180 – x. Next, we can substitute this value into the equation (1/2)y = 2x and then solve for x.
(1/2)(180-x) = 2x.
Multiply both sides by 2 to get rid of the fraction.
(180 – x) = 4x.
Add x to both sides.
180 = 5x.
Divide both sides by 5.
x = 36.
The measure of angle ABC is 36 degrees. However, the original question asks us to find the measure of the complement of ABC, which we denoted previously as z. Because the sum of the measure of an angle and the measure of its complement equals 90, we can write the following equation:
x + z = 90.
Now, we can substitute 36 as the value of x and then solve for z.
36 + z = 90.
Subtract 36 from both sides.
z = 54.
The answer is 54.
Certified Tutor
Certified Tutor
All Basic Geometry Resources











 ?
?



































