All Calculus 1 Resources
Example Questions
Example Question #1 : How To Find Volume Of A Region
Suppose I want to construct a cylindrical container. It costs 5 dollars per square foot to construct the two circular ends and 2 dollars per square foot for the rounded side. If I have a budget of 100 dollars, what's the maximum volume possible for this container?
Write down equations representing the volume(V) and cost of the cylinder.
We want to find the values of 


Plug this into the volume equation
So now 


We can use this 
Now that we found 

Example Question #3911 : Calculus
We have the function and it is used to form a three dimensional figure by rotating it about the line
. Find the volume of that figure from
to
.
Volume is infinite
Imagine a test rectangle with a length of and it is rotated around
to form a cicular disk with area
. The disk has a thickness
so that its volume is
. To find the total volume of the figure, turn this into an integral.
Perform the integration
Example Question #3912 : Calculus
Consider a volume V of height H along some axis, which we will simply call h, such that 


What is 

The volume is approximated by the Riemann sum formed when we stack n layers atop each other with 
In the limit as n gets large, this expression becomes the integral:
Example Question #3913 : Calculus
What is the volume inside the bowl 


Since 

and integrating gives:
Example Question #4 : Volume
The following function:
Is rotated around the 


Note that for a given value of x in the function:
The value of f(x) is the distance between the corresponding point on the curve and the x-axis. If the curve is rotated around the x-axis to create a three-dimensional object, f(x) can be seen as the radius of a circular cross-section of the object for any value of x.
To define the volume of this object, we can view it as a sum of infinitely thin disks stacked along the x-axis:
Note how this follows the formula for the volume of a cylinder or disk

where 

Plugging in our function and range, we can rewrite this as:
or
Integrating this yields

Using the upper bound of 2 and lower bound of 0 we find,

Example Question #3914 : Calculus
Determine the volume for the region bounded by 


In the region bounded by 

Determine which function is the top function. This will be the big radius, and the small radius is represented by the bottom curve. The bounds of the integral are at the intersections of the two bounded functions. Evaluate the integral.
Example Question #3915 : Calculus
The unit circle is described by 




The unit circle is described by 



To find the volume of a region rotated around the 
In our case, this is:
Example Question #1 : How To Find Volume Of A Region
Using the method of cylindrical disks, find the volume of the region of the graph of
revolved around the 
![[0,10]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/371602/gif.latex)





The formula for the volume is given as

where 
As such,

When taking the integral, we will use the inverse power rule which states,

Applying this rule we get

And by the corollary of the first Fundamental Theorem of Calculus,
![\pi\left(\frac{1}{5}x^5\right)\left.\begin{matrix} \, \end{matrix}\right|_{0}^{10}=\pi \left(\left[\frac{1}{5}(10)^5\right]-\left[\frac{1}{5}(0)^5\right]\right)=20000\pi](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/373154/gif.latex)
As such, the volume is

Example Question #1 : How To Find Volume Of A Region
Using the method of cylindrical disks, find the volume of the region of the graph of
revolved around the 
![[0,3]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/371603/gif.latex)





The formula for the volume is given as

where 
As such,

When taking the integral, we will use the inverse power rule which states,

Applying this rule we get

And by the corollary of the first Fundamental Theorem of Calculus,
![\pi\left(\frac{1}{2}x^2\right)\left.\begin{matrix} \, \end{matrix}\right|_{0}^{3}= \pi\left(\left[\frac{1}{2}(3)^2\right]-\left[\frac{1}{2}(0)^2\right]\right)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/373158/gif.latex)
As such, the volume is

Example Question #2 : How To Find Volume Of A Region
Find the volume of the solid shape made by rotating 

![[0,3]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/385876/gif.latex)
Find the volume of the solid shape made by rotating f(x) about the x-axis on the interval
Recall the following formula for volume of a solid shape:
Where A(x) is equal to the the area of a disk made by rotating our function:
So we need to put it all together:
Then, we know that our limits of integration must be 0 and 3, because they are the interval that we are working with.

(Notice that plugging in 0 will yield 0, so we only need to really worry about the 3)
So our answer is:
All Calculus 1 Resources



















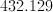


















![V = \int_0^1 \pi ~z~ dz = \pi \left[ \frac{z^2}{2} \right ]_0^1 = \pi \left( \frac{1}{2} - 0 \right ) = \frac{\pi}{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/134552/gif.latex)

















![V=\pi\left[\frac{x^3}{3}-\frac{x^5}{5}\right]_{0}^{1}=\pi\left[\frac{1}{3}-\frac{1}{5}\right] = \frac{2\pi}{15}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/364927/gif.latex)








![V =\pi \left[x-\frac{1}{3}x^3\right]_{-\sqrt{2}/2}^{\sqrt{2}/2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/351943/gif.latex)














![[0,3]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/385877/gif.latex)











