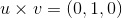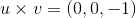All Calculus 3 Resources
Example Questions
Example Question #1 : Cross Product
Let 

Find 
We are trying to find the cross product between 

Recall the formula for cross product.
If 


Now apply this to our situation.
Example Question #1 : Cross Product
Let 

Find 
We are trying to find the cross product between 

Recall the formula for cross product.
If 


Now apply this to our situation.
Example Question #3 : Cross Product
True or False: The cross product can only be taken of two 3-dimensional vectors.
False
True
True
This is true. The cross product is defined this way. The dot product however can be taken for two vectors of dimension n (provided that both vectors are the same dimension).
Example Question #3 : Cross Product
Which of the following choices is true?
By definition, the order of the dot product of two vectors does not matter, as the final output is a scalar. However, the cross product of two vectors will change signs depending on the order that they are crossed. Therefore

Example Question #2 : Cross Product
For what angle(s) is the cross product 
We have the following equation that relates the cross product of two vectors 


From this, we can see that the numerator, or cross product, will be 




Example Question #361 : Calculus 3
Evaluate
None of the other answers
None of the other answers
It is not possible to take the cross product of 

Example Question #112 : Vectors And Vector Operations
Compute 
To evaluate the cross product, we use the determinant formula
So we have

Example Question #4 : Cross Product
Evaluate 
None of the other answers
To evaluate the cross product, we use the determinant formula
So we have

Example Question #9 : Cross Product
Find the cross product of the two vectors.
To find the cross product, we solve for the determinant of the matrix
The determinant equals
As the cross-product.
Example Question #10 : Cross Product
Find the cross product of the two vectors.
To find the cross product, we solve for the determinant of the matrix
The determinant equals
As the cross-product.
Certified Tutor
All Calculus 3 Resources