All Calculus 3 Resources
Example Questions
Example Question #1 : Line Integrals
Write the parametric equations of the line that passes through the points 

First, you must find the vector that is parallel to the line.
This vector is

From the points we were given, this becomes

To form the parametric equations, we need to pick a point that lies on the line we want.
The point 
The vector form of the line is from the following equation

We then rewrite each expression in terms of the variables x, y, and z.
Example Question #2 : Line Integrals
Evaluate the line integral 



Evaluate the line integral 

from

Define the Parametric Equations to Represent
The points given lie on the line 




_________________________________________________________________
The line integral of a function 





Where 


______________________________________________________________
Write the vector 
Differentiate,
The absolute value (magnitude) of this vector is:
Write the function 

Insert everything into Equation (1) noting that the limits of integration will be 



Example Question #1 : Fundamental Theorem Of Line Integrals
Evaluate 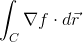


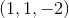

Since there isn't a specific path we need to take, we just evaluate 
Example Question #1 : Line Integrals
Use Green's Theorem to evaluate 




First we need to make sure that the conditions for Green's Theorem are met.
The conditions are met because it is positively oriented, piecewise smooth, simple, and closed under the region (see below).
In this particular case 




We know from Green's Theorem that
So lets find the partial derivatives.
Example Question #1 : Green's Theorem
Use Green's Theorem to evaluate the line integral
over the region R, described by connecting the points 
Using Green's theorem
since the region is oriented clockwise, we would have
which gives us
Example Question #6 : Line Integrals
Use Greens Theorem to evaluate the line integral
over the region connecting the points 
Using Green's theorem

Since the region is oriented clockwise
Example Question #1 : Line Integrals
Compute 
In order to find the divergence, we need to remember the formula.
Divergence Formula:





Now lets apply this to our situation.
Example Question #2 : Line Integrals
Compute 
In order to find the divergence, we need to remember the formula.
Divergence Formula:





Now lets apply this to our situation.
Example Question #3 : Line Integrals
Compute 
In order to find the divergence, we need to remember the formula.
Divergence Formula:





Now lets apply this to our situation.
Example Question #2 : Line Integrals
Find 
In order to find the divergence, we need to remember the formula.
Divergence Formula:





Now lets apply this to our situation.
Certified Tutor
Certified Tutor
All Calculus 3 Resources



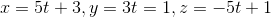
















![=\frac{\sqrt{41}}{4}\left[\frac{5}{8}t^2+\frac{1}{\pi}\sin(\pi t) \right ]_{t=0}^{t=4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/933661/gif.latex)
![=\frac{\sqrt{41}}{4}\left[\frac{5}{8}(16)+\frac{1}{\pi }\sin(4 \pi) -0-\frac{1}{\pi}\sin(0)\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/933662/gif.latex)






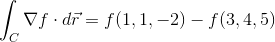

























![\int_C{F}dr=\int \int\left[{\frac{\partial{Q}}{\partial{x}}-\frac{\partial{P}}{\partial{y}}}\right]dA](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/766279/gif.latex)


![\int_C{F}dr=-\int\int\left[\frac{\partial{Q}}{\partial{x}}-\frac{\partial{P}}{\partial{y}}\right]dA](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/766282/gif.latex)







![\int_C F dr=\int\int \left[\frac{\partial{Q}}{\partial{x}}-\frac{\partial{P}}{\partial{y}}\right]dA](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/768557/gif.latex)









































