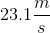In this question, we're told that an unknown gas is held within a container. Connected to this container is a tube open to the atmosphere which also contains a liquid. Based on the image shown, the height difference of the liquid levels, and the atmospheric pressure, we're asked to determine the pressure of the unknown gas inside the container.

This is a fairly straight-forward problem that asks us about pressure. Because of the way the tubing is situated, the pressure from the atmosphere will push down on the right side of the tubing, while the pressure from the unknown gas in the container will push down on the left part of the tubing. Since the liquid level on the left is lower than on the right, we can infer that the gas in the container is "pushing" on the liquid more strongly than the atmosphere on the other side. Consequently, we know that the gas in the container has a pressure greater than atmospheric pressure.

The difference in height of the liquid levels allows us to quantitatively determine how much greater this pressure is. Since the height difference shows up as , we know that the gas in the container is  more than atmospheric pressure.

For this question, we need to understand the relationship between gauge pressure, ambient pressure, and absolute pressure.

The absolute pressure that an object experiences has two components; ambient and gauge pressure. The ambient pressure is an arbitrarily defined reference pressure that acts on the object. Generally, atmospheric pressure at sea level is used as the reference value, which is . The gauge pressure is measured relative to the ambient pressure that has been used as a reference point. Gauge pressure is dependent on the density of the fluid in which the object is submerged together with the distance under which the object is submerged in the fluid.

The equation for absolute pressure can be expressed as follows.

In the above expression,  is one component of the gauge pressure and refers to the distance of the object from the surface of water. As the object is submerged deeper, it will experience a greater gauge pressure and thus a greater absolute pressure.

But what happens if  were doubled from  to , as stated in the question stem? This would certainly cause the gauge pressure to double, but would it cause the absolute pressure to double? The answer is no; there is still the atmospheric pressure to take into account, which maintains the same value in both cases. Because we are increasing the gauge pressure, we know that absolute pressure will increase, but not to the extent of doubling. Thus, we know that it will increase slightly.

This question tests the concept of the continuity equation which stipulates that at steady state the volume flowing into one end of a pipe must be exactly equal to the volume flowing out of the other end. That is, . Note that in this case, we are given the inlet diameter and not cross-sectional area. Thus, we must also find the inlet's cross-sectional area by using the formula for the area of a circle.

To see how a change of radius affects the velocity of a moving fluid, we'll need to take the continuity equation into account.

Even though the radius is not shown in the above expression, remember that area is related to radius.

Or put another way:

When substituted into the continuity equation:

As the above proportionality shows, if the radius were to decrease by a factor of , this would cause the flow rate to decrease by a factor of . To counteract this drop in flow rate, the velocity term would need to increase by a factor of .

The equation for the buoyant force is . The gravitational force is constant. In order for the coconut to float, the buoyant force must be greater than the gravitational force. If the gravitational force is greater than the buoyant force, then the object will sink.

We are given the mass of the baseball outside of the water. Using the weight equation with the gravitational constant being and the mass being , the weight of the baseball outside of the water is 4.905 N. (Be careful and convert the mass of the baseball from grams to kilograms since we are using SI units).

The buoyancy force is the difference of the weight of the baseball when it is in the air and when it is in the water. So subtract the two differences:

Now we use the buoyancy equation:

 where  is the buoyancy force,  is the density of water,  is the volume of the baseball, and  is the gravitational constant. Plug in the known variables and solve for the volume.

and we get