All Common Core: 2nd Grade Math Resources
Example Questions
Example Question #1 : Solve Word Problems Involving Money: Ccss.Math.Content.2.Md.C.8
If I have 

Each dime is worth 

We have three dimes and two pennies.
![\frac{\begin{array}[b]{r}10\cent\\ \ 10\cent\\ +\ 10\cent\end{array}}{ \ \ \ \space 30\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457083/gif.latex)
Example Question #1 : Solve Word Problems Involving Money: Ccss.Math.Content.2.Md.C.8
If I have 

Each dime is worth 

We have five dimes and two pennies.
![\frac{\begin{array}[b]{r}10\cent\\ \ 10\cent\\ 10\cent\\ \ 10\cent\\+\ 10\cent\end{array}}{ \ \ \ \space 50\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457490/gif.latex)
Example Question #161 : How To Add
If I have 

Each quarter is worth 

We have one quarter and three nickels.

Example Question #2 : Solve Word Problems Involving Money: Ccss.Math.Content.2.Md.C.8
If I have 

Each nickel is worth 

We have three nickels and four dimes.
![\frac{\begin{array}[b]{r}5\cent\\ \ 5\cent\\ +\ 5\cent\end{array}}{ \ \ \space 15\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457097/gif.latex)
Example Question #3 : Solve Word Problems Involving Money: Ccss.Math.Content.2.Md.C.8
If I have 

Each penny is worth 
We have three pennies and two quarters.
![\frac{\begin{array}[b]{r}1\cent\\ \ 1\cent\\ +\ 1\cent\end{array}}{ \ \ \ \space 3\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457222/gif.latex)
Example Question #1 : Solve Word Problems Involving Money: Ccss.Math.Content.2.Md.C.8
If I have 

Each penny is worth 
We have six pennies and four nickels.
![\frac{\begin{array}[b]{r}1\cent\\ \ 1\cent\\ 1\cent\\ \ 1\cent\\ 1\cent\\ +\ 1\cent\end{array}}{ \ \ \ \space 6\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457251/gif.latex)
Example Question #4 : Solve Word Problems Involving Money: Ccss.Math.Content.2.Md.C.8
If I have 

Each dime is worth 

We have two dimes and two nickels.
![\frac{\begin{array}[b]{r}10\cent\\ +\ 10\cent\end{array}}{ \ \ \ \space 20\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457237/gif.latex)
Example Question #1 : Solve Word Problems Involving Money: Ccss.Math.Content.2.Md.C.8
If I have 

Each quarter is worth 

We have three quarters and three pennies.
![\frac{\begin{array}[b]{r}25\cent\\ \ 25\cent\\ +\ 25\cent\end{array}}{ \ \ \ \space 75\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457205/gif.latex)
Example Question #431 : Isee Lower Level (Grades 5 6) Quantitative Reasoning
If I have 

Each nickel is worth 

We have four nickels and three dimes.
![\frac{\begin{array}[b]{r}5\cent\\ \ 5\cent\\5\cent\\ +\ 5\cent\end{array}}{ \ \ \ \space 20\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457198/gif.latex)
Example Question #31 : How To Add
If I have 

Each quarter is worth 

We have two quarters and two pennies.
![\frac{\begin{array}[b]{r}25\cent\\ +\ 25\cent\end{array}}{ \ \ \ \space 50\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457244/gif.latex)
Certified Tutor
All Common Core: 2nd Grade Math Resources






![\frac{\begin{array}[b]{r}1\cent\\ +\ 1\cent\end{array}}{ \ \ \ \space 2\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457084/gif.latex)
![\frac{\begin{array}[b]{r}30\cent\\ +\ 2\cent\end{array}}{ \ \ \space 32\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457085/gif.latex)





![\frac{\begin{array}[b]{r}1\cent\\ +\ 1\cent\end{array}}{ \ \ \ \space 2\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457491/gif.latex)
![\frac{\begin{array}[b]{r}50\cent\\ +\ 2\cent\end{array}}{ \ \ \space 52\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457492/gif.latex)





![\frac{\begin{array}[b]{r}5\cent\\ \ 5\cent\\ +\ 5\cent\end{array}}{ \ \ \space 15\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457091/gif.latex)
![\frac{\begin{array}[b]{r}25\cent\\ +\ 15\cent\end{array}}{ \ \ \ \space 40\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457092/gif.latex)





![\frac{\begin{array}[b]{r}10\cent\\ \ 10\cent\\10\cent\\ \ +\ 10\cent\end{array}}{ \ \ \ \space 40\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457098/gif.latex)
![\frac{\begin{array}[b]{r}15\cent\\ +\ 40\cent\end{array}}{ \ \ \ \space 55\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457099/gif.latex)






![\frac{\begin{array}[b]{r}25\cent\\ +\ 25\cent\end{array}}{ \ \ \ \space 50\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457225/gif.latex)
![\frac{\begin{array}[b]{r}3\cent\\ +\ 50\cent\end{array}}{ \ \ \ \space 53\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457227/gif.latex)






![\frac{\begin{array}[b]{r}5\cent\\ \ 5\cent\\ 5\cent\\ +\ 5\cent\end{array}}{ \ \ \space 20\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457252/gif.latex)
![\frac{\begin{array}[b]{r}6\cent\\ +\ 20\cent\end{array}}{ \ \ \ \space 26\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457253/gif.latex)





![\frac{\begin{array}[b]{r}5\cent\\ +\ 5\cent\end{array}}{ \ \ \space 10\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457238/gif.latex)
![\frac{\begin{array}[b]{r}20\cent\\ +\ 10\cent\end{array}}{ \ \ \ \space 30\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457239/gif.latex)

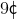



![\frac{\begin{array}[b]{r}1\cent\\ \ 1\cent\\ +\ 1\cent\end{array}}{ \ \ \ \space 3\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457206/gif.latex)
![\frac{\begin{array}[b]{r}75\cent\\ +\ 3\cent\end{array}}{ \ \ \space 78\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457207/gif.latex)





![\frac{\begin{array}[b]{r}10\cent\\ \ 10\cent\\ +\ 10\cent\end{array}}{ \ \ \ \space 30\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457199/gif.latex)
![\frac{\begin{array}[b]{r}20\cent\\ +\ 30\cent\end{array}}{ \ \ \ \space 50\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457200/gif.latex)





![\frac{\begin{array}[b]{r}1\cent\\ +\ 1\cent\end{array}}{ \ \ \ \space 2\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457245/gif.latex)
![\frac{\begin{array}[b]{r}50\cent\\ +\ 2\cent\end{array}}{ \ \ \space 52\cent}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/457246/gif.latex)



