All Common Core: High School - Number and Quantity Resources
Example Questions
Example Question #1 : Rational Exponents: Ccss.Math.Content.Hsn Rn.A.1
Evaluate:
To evaluate this, let's rewrite the problem.
Now lets break down the cube root.
Example Question #2 : Rational Exponents: Ccss.Math.Content.Hsn Rn.A.1
Evaluate:
To evaluate this, let's rewrite the problem.
Now lets break down the square root.
Example Question #3 : Rational Exponents: Ccss.Math.Content.Hsn Rn.A.1
Evaluate:
To evaluate this, let's rewrite the problem.
Now lets break down the square root.
Example Question #4 : Rational Exponents: Ccss.Math.Content.Hsn Rn.A.1
Evaluate:
To solve this, let's reduce the exponent, and then solve.
Example Question #5 : Rational Exponents: Ccss.Math.Content.Hsn Rn.A.1
Evaluate:
One to any power is just 
Example Question #6 : Rational Exponents: Ccss.Math.Content.Hsn Rn.A.1
Evaluate:
To evaluate this, let's rewrite the problem.
Now lets break down the cube root.
Example Question #7 : Rational Exponents: Ccss.Math.Content.Hsn Rn.A.1
Evaluate:
To solve this, let's reduce the exponent, and then solve.
Example Question #8 : Rational Exponents: Ccss.Math.Content.Hsn Rn.A.1
Evaluate:
Zero to any power is just 

Example Question #9 : Rational Exponents: Ccss.Math.Content.Hsn Rn.A.1
Evaluate:
Zero raised to the zero is equal to one, otherwise it is equal to zero.
Example Question #10 : Rational Exponents: Ccss.Math.Content.Hsn Rn.A.1
Evaluate:
The first part to solving this problem is reducing the exponent, and then solving.
All Common Core: High School - Number and Quantity Resources






![64^{\frac{2}{3}}=(\sqrt[3]{64})^2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/977390/gif.latex)
![(\sqrt[3]{64})^2=(\sqrt[3]{4\cdot4\cdot4})^2=(\sqrt[3]{4^3})^2=4^2=16](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/977391/gif.latex)









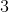






















![64^{\frac{1}{3}}=\sqrt[3]{64}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/975684/gif.latex)
![\sqrt[3]{64}=\sqrt[3]{4\cdot4\cdot4}=\sqrt[3]{4^3}=4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/975685/gif.latex)



























