GRE Math : Mixed / Improper Fractions

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Mixed / Improper Fractions

and are positive integers.

is a multiple of .

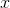
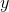
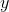
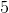
Quantity A: $\frac{x^5}{x^y}$

Quantity B: $x^{5/y}$

Possible Answers:

The relationship cannot be determined.

The two quantities are equal.

Quantity B is greater.

Quantity A is greater.

Correct answer:

The relationship cannot be determined.

Explanation:

Recall that the exponent of the denominator is sutracted from the exponent of the numerator.

Therefore Quantity A is equivalent to x^5–y, and because we would then be comparing an arithmetic operation to a geometric operation, it does not matter whether y is a multiple of 5. The two quantities cannot be compared.

Report an Error

Example Question #2 : Mixed / Improper Fractions

Which of the following is the mixed fraction equivalent to $\frac{19}{3}$ ?

Possible Answers:

$6\frac{3}{5}$

$6\frac{1}{3}$

$\frac{13}{3}$

$8\frac{2}{3}$

$\frac{3}{19}$

Correct answer:

$6\frac{1}{3}$

Explanation:

To begin, notice that using your calculator, you can find:

$\frac{19}{3} = 6.33333...$

Now, the closest even multiple of that is less than is . Therefore, you know that your number is:

$\frac{19}{3}=\frac{18}{3}+\frac{1}{3}$

This is the same as:

$6+\frac{1}{3}$ , or simply, $6\frac{1}{3}$ . This is your mixed fraction.

Report an Error

Example Question #4 : Mixed / Improper Fractions

Which of the following is equivalent to $\frac{82}{4}$ ?

Possible Answers:

$15\frac{1}{2}$

$20\frac{1}{4}$

$15\frac{3}{4}$

$20\frac{3}{8}$

$20\frac{1}{2}$

Correct answer:

$20\frac{1}{2}$

Explanation:

Although there are many ways to convert improper fractions into mixed fractions, the easiest way is to use your calculator to your advantage. Begin by dividing by . This gives you 20.5 . Therefore, you can eliminate all the options that have do not have for their first portion. Next, multiply 0.5 by the denominator (), and get . This means that you have and $\frac{2}{4}$ , or $\frac{1}{2}$ . Thus, your answer is $20\frac{1}{2}$ .

Report an Error

Example Question #1 : How To Find Out A Mixed Fraction From An Improper Fraction

Quantity A: $\frac{490}{12}$

Quantity B: $40\frac{5}{6}$

Which of the following is true?

Possible Answers:

Quantity B is larger.

Quantity A is larger.

The relationship of the two quantities cannot be determined based on the information provided.

The two quantities are equal

Correct answer:

The two quantities are equal

Explanation:

Though there are several ways you could solve this, let's convert the improper fraction into a mixed one so we can compare them. Start by dividing 490 by . This gives you 40.833333...

Now, since we know that the two numbers have the same whole-number value, we need to compare their decimal portions. Compare 0.833333... to $\frac{5}{6}$ . The latter is indeed Therefore, the two values are equal.

Report an Error

Example Question #1522 : Act Math

Write $71\frac{5}{7}$ as an improper fraction.

Possible Answers:

$\frac{355}{7}$

$\frac{76}{8}$

$\frac{76}{7}$

$\frac{360}{7}$

$\frac{502}{7}$

Correct answer:

$\frac{502}{7}$

Explanation:

To find the improper fraction value, we must effectively add together 71 and ⁵/₇. To do this, we will give 71 a denominator of 7; therefore, we are transforming ⁷¹/₁ to ^x/₇. The shortest way to do this is to multiply by ⁷/₇ (which really is 1); therefore, 71 = 71 * (⁷/₇) = ⁴⁹⁷/₇.

Now add them: ^{(497 + 5)}/₇ = ⁵⁰²/₇

Report an Error

Example Question #1523 : Act Math

Which of the following improper fractions is equivalent to $14\frac{2}{5}$ ?

Possible Answers:

$\frac{70}{5}$

$\frac{72}{5}$

$\frac{24}{5}$

$\frac{84}{3}$

$\frac{16}{5}$

Correct answer:

$\frac{72}{5}$

Explanation:

To find an improper fraction, you need to multiply the whole number that you have by the denominator of the associated fraction. For our problem, this means that you will multiply by , getting . Next, you add this to the numerator of your fraction, giving you 70+2 , or . Finally, you place this over your original denominator, giving you:

$\frac{72}{5}$

Report an Error

Example Question #1 : How To Find Out An Improper Fraction From A Mixed Fraction

Which of the following improper fractions is equivalent to $27\frac{4}{19}$ ?

Possible Answers:

$\frac{517}{19}$

$\frac{49}{19}$

$\frac{481}{19}$

$\frac{31}{19}$

$\frac{813}{17}$

Correct answer:

$\frac{517}{19}$

Explanation:

To find an improper fraction, you need to multiply the whole number that you have by the denominator of the associated fraction. For our problem, this means that you will multiply by , getting 513 . Next, you add this to the numerator of your fraction, giving you 513+4 , or 517 . Finally, you place this over your original denominator, giving you:

$\frac{517}{19}$

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Seattle, Statistics Tutors in Houston, GRE Tutors in Denver, Biology Tutors in San Francisco-Bay Area, Chemistry Tutors in San Diego, SSAT Tutors in Atlanta, Statistics Tutors in Chicago, Physics Tutors in Philadelphia, Math Tutors in Los Angeles, Biology Tutors in Atlanta

Popular Courses & Classes

MCAT Courses & Classes in Boston, MCAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Denver, ISEE Courses & Classes in Los Angeles, ACT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Houston, GMAT Courses & Classes in Philadelphia, Spanish Courses & Classes in New York City, Spanish Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in New York City

Popular Test Prep

ISEE Test Prep in Houston, GRE Test Prep in New York City, LSAT Test Prep in Philadelphia, ISEE Test Prep in Boston, ISEE Test Prep in Seattle, SAT Test Prep in Washington DC, ISEE Test Prep in San Diego, LSAT Test Prep in Houston, GMAT Test Prep in Philadelphia, SAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : Mixed / Improper Fractions

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #1 : Mixed / Improper Fractions

Example Question #2 : Mixed / Improper Fractions

Example Question #4 : Mixed / Improper Fractions

Example Question #1 : How To Find Out A Mixed Fraction From An Improper Fraction

Example Question #1522 : Act Math

Example Question #1523 : Act Math

Example Question #1 : How To Find Out An Improper Fraction From A Mixed Fraction

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details