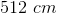GRE Math : How to find the perimeter of a square
Study concepts, example questions & explanations for GRE Math
All GRE Math Resources
Example Questions
Example Question #1361 : Gre Quantitative Reasoning
What is the perimeter of a square that has an area of 81?
40.5
9
18
36
36
36
A square has four equal sides and its area = side2. Therefore, you can find the side length by taking the square root of the area √81 = 9. Then, find the perimeter by multiplying the side length by 4:
4 * 9 = 36
Example Question #1 : How To Find The Perimeter Of A Square
The radius of the circle is 2 inches. What is the perimeter of the inscribed square?
The center of an inscribed square lies on the center of the circle. Thus, the line joining the center to a vertex of the square is also the radius. If we join the center with two adjacent vertices we can create a 45-45-90 right isosceles triangle, where the diagonal of the square is the hypotenuse. Since the radius is 2, the hypotenuse (a side of the square) must be 
Finally, the perimeter of a square is 
Example Question #2 : How To Find The Perimeter Of A Square
The diagram above represents a square ABCD with a semi-circle directly attached to its side. If the area of the figure is 16 + 2π, what is its outer perimeter?
16
16 + 2π
12 + 2π
20π
None of the other answers
12 + 2π
We know that our area can be represented by the following equation:
Instead of solving the algebra, you should immediately note several things. 16 = 42 and 4 = 22. If the side of the square is 4, then s = 4 would work out as:
which is just what we need.
With s = 4, we know that 3 sides of our figure will have a perimeter of 12. The remaining semicircle will be one half of the circumference of a circle with diameter of 4; therefore it will be 0.5 * 4 * π or 2π.
Therefore, the outer perimeter of our figure is 12 + 2π.
Example Question #171 : Plane Geometry
A square table has an area of 
If 
We start by writing the equations for the area and perimeter in terms of a side of length s.
Then, substitute both of these expressions into the given equation to solve for side length.
Finally, since four sides make up the perimeter, we substitue s back into our perimeter equation and solve for P.
Example Question #3 : How To Find The Perimeter Of A Square
The diagonal of square 
First we must convert to inches.
The diagonal of a square divides the square into two isosceles-right triangles. Using the Pythagorean Theorem, we know that 
This gives us 
Therefore, the perimeter of square 
All GRE Math Resources
