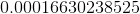GRE Math : Fractions and Percentage
Study concepts, example questions & explanations for GRE Math
All GRE Math Resources
Example Questions
Example Question #1 : Percentage
What percentage of a solution is blood if it contains 
First, you must find the total amount of solution. This is 
Now, the percentage of the solution that is blood can be represented:
This is the same as 
Example Question #1 : Percentage
What is the percentage increase of an account that began with a balance of 
Recall that the formula for percentage increase is:
For our numbers, this would be:
Recall that to find a percentage from a decimal, you multiply by 
Example Question #1 : Percentage
If one of the employees across both industries were to be selected at random, what is the probability that the employee will be a construction industry worker who stayed in the same role for 5 years or more?
65%
17%
20%
26%
10%
26%
The first step is to figure out the percentage of construction employees that have stayed in the same role for 5 years or more—this would include both the "5 to 9 year" and "10+ years" ranges. This would be 0.25 + 0.4 = 65% of all construction employees. To convert to the number of employees, we take the percentage of their total, 0.65 * 8,000,000 = 5,200,000 workers. However, since the probability we are attempting to find is of workers between both industries, we must add the 8 million to the 12 million = 20 million workers total. 5,200,000/20,000,000 = 0.26, or a 26% chance.
Example Question #2 : Percentage
For every 1000 cookies baked, 34 are oatmeal raisin.
Quantity A: Percent of cookies baked that are oatmeal raisin
Quantity B: 3.4%
Quantity B is greater
Quantity A is greater
The two quantities are equal.
The relationship cannot be determined from the information given.
The two quantities are equal.
Simplify Quantity A by dividing the number of oatmeal raisin cookies by the total number of cookies to find the percentage of oatmeal raisin cookies. Since a percentage is defined as being out of 100, either multiply the resulting decimal by 100 or reduce the fraction until the denominator is 100. You will find that the two quantities are equal.
Example Question #3 : Percentage
50 students took an exam. There were 4 A's, 9 B's, 15 C's, 8 D's, and the rest of the students failed. What percent of the students failed?
which equals 28%.
Example Question #4 : Percentage
Column A: 
Column B:
The relationship cannot be determined from the given information.
Column B is greater.
The two quantities are equal.
Column A is greater.
Column B is greater.
2/5% = 0.40% = 0.004. Therefore, Column B is greater.
Example Question #4 : Percentage
Quantity A:
Quantity B:
Quantity A is greater.
The relationship cannot be determined.
The two quantities are equal.
Quantity B is greater.
Quantity B is greater.
To do this problem, translate each expression into mathematical terms:
Quantity B is greater.
Example Question #1 : Percentage
Quantity A: 20% of
Quantity B: 30% of
The relationship cannot be determined.
Quantity A is greater.
Quantity B is greater.
The two quantities are equal.
Quantity B is greater.
To solve this problem, consider writing the quantities in terms of only fractions:
Quantity A: 20% of
Quantity B: 30% of
Quantity B has the smaller denominator for an equal numerator. There is no need for calculation beyond this, and time on the GRE would be best spent elsewhere.
Quantity B is greater.
All GRE Math Resources
