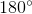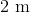Call Now to Set Up Tutoring:

(888) 888-0446

GRE Subject Test: Physics : Optics

Study concepts, example questions & explanations for GRE Subject Test: Physics

Create An Account

All GRE Subject Test: Physics Resources

33 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Polarization

A beam of unpolarized light passes through two linear polarizers whose polarization axes are at an angle theta with each other. The light initially has an intensity I_o , and has an intensity of $\frac{3}{8}I_o$ after passing through both polarizes. Find $\theta$ ?

Possible Answers:

$45^\circ$

$30^\circ$

$180^\circ$

$60^\circ$

$90^\circ$

Correct answer:

$30^\circ$

Explanation:

Initially unpolarized light passing though a linear polarizer decreases in intensity by a factor of two:

$I=\frac{I_o}{2}$

Malus's Law gives the change in intensity of polarized light passing through a linear polarizer in terms of the change in angle of polarization:

$I=I_o\cos^2\theta$

Combining the two equations, we get:

$I=\frac{I_o}{2}\cos^2\theta$

Solving for $\theta$ :

$\theta=\cos^{-1}(\sqrt{\frac{2I}{I_o}})=\cos^{-1}(\sqrt{\frac{2\frac{3I_o}{8}}{I_o}})=\cos^{-1}(\frac{\sqrt{3}}{2}) =30^\circ$

Report an Error

Example Question #4 : Electromagnetics, Waves, And Optics

A beam of light travels through a medium with index of refraction n_1=2.4 until it reaches an interface with another material, with index of refraction n_2=1.2 . No light is transmitted into the second material. At what angle (measured from the plane of the interface between the two materials) does the beam hit the second material?

Possible Answers:

$60^\circ$

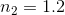
This situation is impossible.

$30^\circ$

$90^\circ$

$45^\circ$

Correct answer:

$60^\circ$

Explanation:

Total internal reflection occurs at the angle:

$\theta=\sin^{-1}(\frac{n_2}{n_1})=\sin^{-1}(\frac{1.2}{2.4})=\sin^{-1}(\frac{1}{2})=30^o$

However, this angle is measured from a line normal to the plane of the interface; the angle we want, therefore, is 90-30 , which is $60^\circ$ .

Report an Error

Example Question #1 : Lenses

The focal length of a thin convex lens is $10\textup{ cm}$ . A candle is placed $25\textup{ cm}$ to the left of the lens. Approximately where is the image of the candle?

Possible Answers:

$17\textup{ cm}$ to the right of the lens

No image is created

$7\textup{ cm}$ to the left of the lens

$7\textup{ cm}$ to the right of the lens

$17\textup{ cm}$ to the left of the lens

Correct answer:

$17\textup{ cm}$ to the right of the lens

Explanation:

Because the object is beyond 2 focal lengths of the lens, the image must be between 1 and 2 focal lengths on the opposite side. Therefore, the image must be between $10-20\textup{ cm}$ on the right side of the lens.

Alternatively, one can apply the thin lens equation:

$\frac{1}{f}=\frac{1}{d_o}+\frac{1}{d_i}$

Where d_o is the object distance $(25\textup{ cm})$ and is the focal length $(10\textup{ cm})$ . Plug in these values and solve.

$\frac{1}{10}=\frac{1}{25} +\frac{1}{d_i}$

$\frac{1}{d_i}=\frac{5}{50}-\frac{2}{50}=\frac{3}{50}$

$d_i=\frac{50}{3}\approx 17\textup{ cm}$

Report an Error

Example Question #1 : Lenses

A candle $5\textup{ cm}$ tall is placed $25\textup{ cm}$ to the left of a thin convex lens with focal length $10\textup{ cm}$ . What is the height and orientation of the image created?

Possible Answers:

$\frac{17}{85} \textup{ cm}$ , upright

No image is created.

$\frac{85}{17} \textup{ cm}$ , upright

$\frac{85}{17} \textup{ cm}$ , inverted

$\frac{17}{85} \textup{ cm}$ , inverted

Correct answer:

$\frac{85}{17} \textup{ cm}$ , inverted

Explanation:

First, find the image distance d_i from the thin lens equation:

$\frac{1}{f}=\frac{1}{d_o}+\frac{1}{d_i}$

$\frac{1}{10}=\frac{1}{25}+\frac{1}{d_i}$

$\frac{5}{50}-\frac{2}{50}=\frac{1}{d_i}$

$d_i\approx 17\textup{ cm}$

Magnification of a lens is given by:

$M=-\frac{d_i}{d_o}=\frac{h_i}{h_o}$

Where h_i and are the image height and object height, respectively. The given object height is $5\textup{ cm}$ , which we can use to solve for the image height:

$h_i=-\frac{d_ih_o}{d_o}=-\frac{85}{17}\textup{ cm}$

Because the sign is negative, the image is inverted.

Report an Error

Example Question #44 : Gre Subject Test: Physics

Sirius is a binary star system, consisting of two white dwarfs with an angular separation of 3 arcseconds. What is the approximate minimum diameter lens needed to resolve the two stars in Sirius for an observation at $600\textup{ nm}$ ?

Possible Answers:

$5\textup{ mm}$

$50\textup{ m}$

$5\textup{ cm}$

$5\textup{ m}$

$50\textup{ cm}$

Correct answer:

$5\textup{ cm}$

Explanation:

The Rayleigh Criterion gives the diffraction limit on resolution of a particular lens at a particular wavelength:

$\theta=1.22\frac{\lambda}{D}$

Where theta is the angular resolution in radians, $\lambda$ is the wavelength of light, and is the diameter the lens in question. Solving for and converting 3 arcseconds into radians, one can approximate the diameter to be about $5\textup{ cm}$ :

$D=1.22\frac{\lambda}{\theta}$

$D=1.22\frac{600*10^{-9}}{1.45*10^{-5}}$

$D=0.05\textup{ m}$

Report an Error

Example Question #1 : Mirrors

A reflective sphere has a diameter of $1\textup{ m}$ . The surface of the sphere makes a convex spherical mirror; what is its focal point?

Possible Answers:

$-25 \textup{ cm}$

$-50 \textup{ cm}$

$25 \textup{ cm}$

$2 \textup{ m}$

$50 \textup{ cm}$

Correct answer:

$-25 \textup{ cm}$

Explanation:

The focal length of a spherical mirror is one half of the radius, which is one quarter of the diameter. In the case of convex mirrors, the focal point is considered behind the surface, which gives the answer its negative sign.

Report an Error

View Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

View Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View Tutors

Austin
Certified Tutor

University of Arizona, Bachelor of Science, Physiology.

All GRE Subject Test: Physics Resources

33 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in Dallas Fort Worth, MCAT Tutors in Seattle, Statistics Tutors in San Diego, SSAT Tutors in Denver, English Tutors in Los Angeles, Math Tutors in Los Angeles, Algebra Tutors in Chicago, GRE Tutors in Dallas Fort Worth, LSAT Tutors in Denver, ACT Tutors in Dallas Fort Worth

Popular Courses & Classes

MCAT Courses & Classes in Denver, GMAT Courses & Classes in New York City, GMAT Courses & Classes in Miami, ACT Courses & Classes in Chicago, Spanish Courses & Classes in Houston, SAT Courses & Classes in Seattle, MCAT Courses & Classes in Philadelphia, SSAT Courses & Classes in Washington DC, GMAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Denver

Popular Test Prep

ACT Test Prep in Chicago, LSAT Test Prep in Chicago, GRE Test Prep in Houston, ISEE Test Prep in New York City, GMAT Test Prep in Chicago, ISEE Test Prep in Houston, LSAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Seattle, LSAT Test Prep in New York City, SSAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

GRE Subject Test: Physics : Optics

Study concepts, example questions & explanations for GRE Subject Test: Physics

All GRE Subject Test: Physics Resources

Example Questions

Example Question #1 : Polarization

Example Question #4 : Electromagnetics, Waves, And Optics

Example Question #1 : Lenses

Example Question #1 : Lenses

Example Question #44 : Gre Subject Test: Physics

Example Question #1 : Mirrors

All GRE Subject Test: Physics Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: