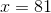All High School Math Resources
Example Questions
Example Question #1 : Understanding Quadratic Equations
Solve the following equation using the quadratic form:
Factor the equation and solve:

or
Therefore there are four answers:
Example Question #2 : Understanding Quadratic Equations
Solve the following equation using the quadratic form:
Factor the equation and solve:

or
This has no solutions.
Therefore there is only one answer:
Example Question #1 : Quadratic Equations And Inequalities
Evaluate
In order to evaluate 
Multiply terms by way of FOIL method.
Now multiply and simplify.
Example Question #2 : Quadratic Equations And Inequalities
Evaluate
In order to evaluate 
Multiply terms by way of FOIL method.
Now multiply and simplify, paying attention to signs.
Example Question #1 : Quadratic Equations And Inequalities
Evaluate
In order to evaluate 
Multiply terms by way of FOIL method.
Now multiply and simplify, paying attention to signs.
Example Question #2 : Quadratic Equations And Inequalities
Evaluate
In order to evaluate 
Multiply terms by way of FOIL method.
Now multiply and simplify, paying attention to signs.
Example Question #3 : Quadratic Equations And Inequalities
FOIL 
Remember FOIL stands for First Outer Inner Last. That means we can take 

Simplify to get 
Example Question #4 : Quadratic Equations And Inequalities
FOIL 


Remember that FOIL stands for First Outer Inner Last.
For this problem, that would be 
Simplify that to 
Example Question #1 : Quadratic Equations And Inequalities
FOIL 
Remember that FOIL stands for First Outer Inner Last.
For this problem that would give us:
Simplify.
Example Question #5 : Quadratic Equations And Inequalities
FOIL 
Remember that FOIL stands for First Outer Inner Last.
For this problem that would give us:
Simplify:
All High School Math Resources