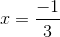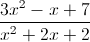Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Rational Expressions

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Understanding Rational Expressions

Solve:

If varies directly as , and x=7 when y=21 , find when y=-5 .

Possible Answers:

$x=\frac{-1}{3}$

$x=\frac{-7}{3}$

$x=\frac{-11}{3}$

$x=\frac{-13}{3}$

$x=\frac{-5}{3}$

Correct answer:

$x=\frac{-5}{3}$

Explanation:

The formula for a direct variation is:

$\frac{x_1}{x_2}=\frac{y_1}{y_2}$

Plugging in our values, we get:

$\frac{7}{x}=\frac{21}{-5}$

21x=-35

$x= \frac{-5}{3}$

Report an Error

Example Question #2 : Understanding Rational Expressions

If two boxes have the same depth and capacity, the length is inversely proportional to the width. One box is $60\ cm$ long and $40\ cm$ wide. A second box (same depth and capacity) is $5\ cm$ long. How wide is it?

Possible Answers:

$460\ cm$

$480\ cm$

$470\ cm$

$450\ cm$

$490\ cm$

Correct answer:

$480\ cm$

Explanation:

The formula for an indirect variation is:

$\frac{x_1}{x_2}=\frac{y_2}{y_1}$

Plugging in our values, we get:

$\frac{60\ cm}{5\ cm}=\frac{y}{40\ cm}$

$5y=2400\ cm$

$y=480\ cm$

Report an Error

Example Question #1 : Adding And Subtracting Rational Expressions

Simplify $\frac{x+2}{x-1}+\frac{x-5}{x+3}$

Possible Answers:

$\frac{3x^{2}-x+7}{x^{2}+2x+2}$

$\frac{2x^{2}-5x+6}{x^{2}-2x+3}$

$\frac{3x^{2}+5x-6}{x^{2}-3x+2}$

$\frac{2x^{2}-x+11}{x^{2}+2x-3}$

$\frac{4x^{2}-3x+5}{x^{2}+3x-2}$

Correct answer:

$\frac{2x^{2}-x+11}{x^{2}+2x-3}$

Explanation:

This is a more complicated form of $\frac{1}{2}+\frac{1}{3}= \frac{3}{6}+\frac{2}{6}=\frac{5}{6}$

Find the least common denominator (LCD) and convert each fraction to the LCD, then add the numerators. Simplify as needed.

$\frac{x+2}{x-1}+\frac{x-5}{x+3}=\frac{x+2}{x-1}\cdot \frac{x+3}{x+3}+\frac{x-5}{x+3}\cdot \frac{x-1}{x-1}$

which is equivalent to $\frac{(x+2)\cdot (x+3)+(x-5)\cdot (x-1)}{(x+3)\cdot (x-1)}$

Simplify to get $\frac{2x^{2}-x+11}{x^{2}+2x-3}$

Report an Error

Example Question #2 : Simplifying Rational Expressions

Divide and simplify the following rational expression:

$\frac{x^2+7x+10}{x+2}\div \frac{x^2+2x-15}{x^2-5x+6}$

Possible Answers:

x+2

x-2

x+1

x-3

x-1

Correct answer:

x-2

Explanation:

Multiply by the reciprocal of the second expression:

$\frac{x^2+7x+10}{x+2}\div \frac{x^2+2x-15}{x^2-5x+6}$

$\frac{x^2+7x+10}{x+2}\cdot \frac{x^2-5x+6}{x^2+2x-15}$

Factor the expressions:

$\frac{(x+5)(x+2)}{x+2}\cdot \frac{(x-3)(x-2)}{(x-3)(x+5)}$

Remove common terms:

$\frac{\mathbf{(x+5)(x+2)}}{\mathbf{x+2}}\cdot \frac{\mathbf{(x-3)}(x-2)}{\mathbf{(x-3)(x+5)}}$

x-2

Report an Error

Example Question #1 : Simplifying Rational Expressions

Add and simplify the following rational expression:

$3n+1+\frac{1}{3n-1}$

Possible Answers:

$\frac{9n^2}{3n-1}$

$\frac{6n^2}{3n-1}$

$\frac{3n^2}{2n-1}$

$\frac{3n^2}{3n-1}$

$\frac{6n^2}{2n-1}$

Correct answer:

$\frac{9n^2}{3n-1}$

Explanation:

Begin by multiplying the left term by $\frac{3n-1}{3n-1}$ :

$3n+1+\frac{1}{3n-1}$

$3n+1 (\frac{3n-1}{3n-1})+\frac{1}{3n-1}$

Simplify:

$\frac{(3n+1)(3n-1)+1}{3n-1}$

$\frac{9n^2-1+1}{3n-1}$

$\frac{9n^2}{3n-1}$

Report an Error

Example Question #1 : Simplifying Rational Expressions

Simplify the following rational expression:

$\frac{\frac{x+y}{x}}{\frac{1}{x}+\frac{1}{y}}$

Possible Answers:

$\frac{x}{y}$

$\frac{y}{x}$

$\frac{1}{x}$

Correct answer:

Explanation:

Begin by combining the terms in the denominator:

$\frac{\frac{x+y}{x}}{\frac{1}{x}+\frac{1}{y}}$

$\frac{\frac{x+y}{x}}{\frac{x+y}{xy}}$

Multiply by the reciprocal of the denominator:

$\frac{x+y}{x} \cdot \frac{xy}{x+y}$

Remove like terms:

$\frac{\mathbf{x+y}}{\mathbf{x}} \cdot \frac{\boldsymbol{x}y}{\mathbf{x+y}}$

Report an Error

Example Question #3 : Simplifying Rational Expressions

Simplify the following rational expression:

$\frac{n+5+\frac{3}{n+1}}{n-1-\frac{3}{n+1}}$

Possible Answers:

$\frac{n+4}{n-2}$

$\frac{n+3}{n-1}$

$\frac{n+4}{n-1}$

$\frac{n+3}{n-2}$

Correct answer:

$\frac{n+4}{n-2}$

Explanation:

Create a common denominator of (n+1) in both the numerator and denominator:

$\frac{n+5+\frac{3}{n+1}}{n-1-\frac{3}{n+1}}$

$\frac{\frac{(n+5)(n+1)+3}{n+1}}{\frac{(n-1)(n+1)-3}{n+1}}$

Multiply by the reciprocal of the denominator:

$\frac{(n+5)(n+1)+3}{n+1}\cdot \frac{n+1}{(n-1)(n+1)-3}$

Simplify:

$\frac{n^2+6n+8}{n+1}\cdot \frac{n+1}{n^2-4}$

$\frac{(n+4)(n+2)}{n+1}\cdot \frac{n+1}{(n-2)(n+2)}$

Remove common terms:

$\frac{(n+4)\mathbf{(n+2)}}{\mathbf{n+1}}\cdot \frac{\mathbf{n+1}}{(n-2)(\mathbf{n+2})}$

$\frac{n+4}{n-2}$

Report an Error

Example Question #4 : Simplifying Rational Expressions

Multiply and simplify the following rational expression:

$\frac{a^3-b^3}{b^2-a^2} \cdot \frac{a+b}{a^2+ab+b^2}$

Possible Answers:

Correct answer:

Explanation:

Factor the expression:

$\frac{(a-b)(a^2+ab+b^2)(a+b)}{(b-a)(b+a)(a^2+ab+b^2)}$

Remove like terms:

$\frac{(a-b)(\mathbf{a^2+ab+b^2})(\mathbf{a+b})}{(b-a)(\mathbf{b+a})(\mathbf{a^2+ab+b^2})}$

$\frac{a-b}{b-a}=\frac{-1(b-a)}{b-a}=-1$

Report an Error

Example Question #5 : Simplifying Rational Expressions

Divide and simplify the following rational expression:

$\frac{x^2-11x+24}{x^2-18x+80}\div \frac{x^2-9x+20}{x^2-15x+50}$

Possible Answers:

$\frac{x-3}{x-4}$

$\frac{x-5}{x-4}$

$\frac{x-4}{x-5}$

$\frac{x-4}{x-3}$

$\frac{x-3}{x-5}$

Correct answer:

$\frac{x-3}{x-4}$

Explanation:

Multiply by the inverse of the denominator:

$\frac{x^2-11x+24}{x^2-18x+80}\div \frac{x^2-9x+20}{x^2-15x+50}$

$\frac{x^2-11x+24}{x^2-18x+80}\cdot \frac{x^2-15x+50}{x^2-9x+20}$

Factor:

$\frac{(x-8)(x-3)}{(x-8)(x-10)}\cdot \frac{(x-5)(x-10)}{(x-5)(x-4)}$

Remove like terms:

$\frac{(\mathbf{x-8})(x-3)}{(\mathbf{x-8})(\mathbf{x-10})}\cdot \frac{(\mathbf{x-5})(\mathbf{x-10})}{(\mathbf{x-5})(x-4)}$

$\frac{x-3}{x-4}$

Report an Error

Example Question #1 : Rational Expressions

Solve the following rational expression:

$\frac{y}{y-3}+\frac{6}{y+3}=1$

Possible Answers:

y=1

y=3

y=2

$y=\frac{1}{2}$

$y=\frac{1}{3}$

Correct answer:

y=1

Explanation:

Multiply the equation by (y-3)(y+3) :

$\frac{y}{y-3}+\frac{6}{y+3}=1$

y(y+3)+6(y-3)=1(y-3)(y+3)

y^2+3y+6y-18 = y^2-9

9y=9

y=1

Report an Error

View Tutors

Lauren
Certified Tutor

University of Mississippi, Masters in Education, Education.

View Tutors

Masoud
Certified Tutor

University of Guilan,, Bachelor of Science, Biological/Biosystems Engineering. University of Tehran, Master of Science, Anima...

View Tutors

Arthi
Certified Tutor

Emory University, Master of Science, Epidemiology.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in New York City, Reading Tutors in Phoenix, SAT Tutors in Miami, ACT Tutors in Denver, SAT Tutors in Dallas Fort Worth, Statistics Tutors in Los Angeles, SSAT Tutors in Los Angeles, Chemistry Tutors in Seattle, GRE Tutors in Denver, Computer Science Tutors in New York City

Popular Courses & Classes

ACT Courses & Classes in Philadelphia, GMAT Courses & Classes in Chicago, ISEE Courses & Classes in San Diego, GMAT Courses & Classes in San Diego, ACT Courses & Classes in San Diego, GRE Courses & Classes in San Diego, LSAT Courses & Classes in Denver, Spanish Courses & Classes in Chicago, ACT Courses & Classes in Seattle, GRE Courses & Classes in Denver

Popular Test Prep

GRE Test Prep in Boston, ISEE Test Prep in Los Angeles, GMAT Test Prep in Seattle, SSAT Test Prep in Phoenix, GMAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Houston, MCAT Test Prep in Atlanta, ACT Test Prep in Philadelphia, LSAT Test Prep in Denver, SSAT Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Rational Expressions

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Understanding Rational Expressions

Example Question #2 : Understanding Rational Expressions

Example Question #1 : Adding And Subtracting Rational Expressions

Example Question #2 : Simplifying Rational Expressions

Example Question #1 : Simplifying Rational Expressions

Example Question #1 : Simplifying Rational Expressions

Example Question #3 : Simplifying Rational Expressions

Example Question #4 : Simplifying Rational Expressions

Example Question #5 : Simplifying Rational Expressions

Example Question #1 : Rational Expressions

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: