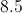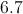All High School Math Resources
Example Questions
Example Question #1 : How To Find The Length Of The Diagonal Of A Square
What is the length of a diagonal of a square with a side length 
A square is comprised of two 45-45-90 right triangles. The hypotenuse of a 45-45-90 right triangle follows the rule below, where 
In this instance, 
Example Question #1 : Squares
A square has sides of 
To find the diagonal of the square, we effectively cut the square into two 
The pattern for the sides of a 

Since two sides are equal to 

Therefore, the diagonal (the hypotenuse) will have a length of 
Example Question #2 : Squares
A square has sides of 
To find the diagonal of the square, we effectively cut the square into two 
The pattern for the sides of a 

Since two sides are equal to 

Therefore, the diagonal (the hypotenuse) will have a length of 
Example Question #2 : How To Find The Length Of The Diagonal Of A Square
What is the length of the diagonal of a square with a side length of 
To find the diagonal of a square, we must use the side length to create a 90 degree triangle with side lengths of 

Pythagorean’s Theorem states , where a and b are the legs and c is the hypotenuse.
Take 



After squaring the numbers, add them together:
Once you have the sum, take the square root of both sides:
Simplify to find the answer: 

Example Question #1 : How To Find The Length Of The Diagonal Of A Square
What is the length of the diagonal of a 7-by-7 square? (Round to the nearest tenth.)
To find the diagonal of a square we must use the side lengths to create a 90 degree triangle with side lengths of 7 and a hypotenuse which is equal to the diagonal.
We can use the Pythagorean Theorem here to solve for the hypotenuse of a right triangle.
The Pythagorean Theorem states , where a and b are the sidelengths and c is the hypotenuse.
Plug the side lengths into the equation as 

Square the numbers:
Add the terms on the left side of the equation together:
Take the square root of both sides:
Therefore the length of the diagonal is 9.9.
Example Question #2 : Squares
The perimeter of a square is 48. What is the length of its diagonal?
Perimeter = side * 4
48 = side * 4
Side = 12
We can break up the square into two equal right triangles. The diagonal of the sqaure is then the hypotenuse of these two triangles.
Therefore, we can use the Pythagorean Theorem to solve for the diagonal:
Example Question #1 : Squares
ABCD and EFGH are squares such that the perimeter of ABCD is 3 times that of EFGH. If the area of EFGH is 25, what is the area of ABCD?
5
15
25
75
225
225
Assign variables such that
One side of ABCD = a
and One side of EFGH = e
Note that all sides are the same in a square. Since the perimeter is the sum of all sides, according to the question:
4a = 3 x 4e = 12e or a = 3e
From that area of EFGH is 25,
e x e = 25 so e = 5
Substitute a = 3e so a = 15
We aren’t done. Since we were asked for the area of ABCD, this is a x a = 225.
Example Question #1 : How To Find The Area Of A Square
A square has an area of 36. If all sides are doubled in value, what is the new area?
72
108
132
144
48
144
Let S be the original side length. S*S would represent the original area. Doubling the side length would give you 2S*2S, simplifying to 4*(S*S), giving a new area of 4x the original, or 144.
Example Question #231 : Plane Geometry
If the perimeter of a square is equal to twice its area, what is the length of one of its sides?
Area of a square in terms of each of its sides:
Area = S x S
Perimeter of a square:
Perimeter = 4S
So if 'the perimeter of a square is equal to twice its area':
2 x Area = Perimeter
2 x [S x S] = [4S]; divide by 2:
S x S = 2S; divide by S:
S = 2
Example Question #2 : Squares
Freddie is building a square pen for his pig. He plans to buy x feet of fencing to build the pen. This will result in a pen with an area of p square feet. Unfortunately, he only has enough money to buy one third of the planned amount of fencing. Which expression represents the area of the pen he can build with this limited amount of fencing?
p/9
3p
p/3
p/6
9p
p/9
If Freddie uses x feet of fencing makes a square, each side must be x/4 feet long. The area of this square is (x/4)2 = x2/16 = p square feet.
If Freddie uses one third of x feet of fencing makes a square, each side must be x/12 feet long. The area of this square is (x/12)2 = x2/144 = 1/9(x2/16) = 1/9(p) = p/9 square feet.
Alternate method:
The scale factor between the small perimeter and the larger perimeter = 1 : 3. Since we're comparing area, a two-dimensional measurement, we can square the scale factor and see that the ratio of the areas is 12 : 32 = 1 : 9.
Certified Tutor
All High School Math Resources