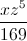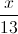First, multiply out the second expression so that you get \(\displaystyle 8y^3\).

Then, multiply your like terms, taking care to remember that when multiplying terms that have the same base, you add the exponents. Thus, you get \(\displaystyle 24x^9y^{12}\).

Focus on each pair of like terms. The \(\displaystyle y's\) completely cancel out, there is one \(\displaystyle x\) left on top, and five \(\displaystyle z's\) left on the bottom. 

\(\displaystyle \frac{13}{169}\) reduces to \(\displaystyle \frac{1}{13}\).

Put that all together to get \(\displaystyle \frac{xz^5}{13}\). 

Put the negative exponent on the bottom so that you have \(\displaystyle \frac{x^{12}}{x^{6}}\) which simplifies further to \(\displaystyle x^{6}\).

Use the FOIL method (First, Outer, Inner, Last):

\(\displaystyle x * 2x = 2x^2\)

\(\displaystyle x * 4 = 4x\)

\(\displaystyle -4 * 2x = -8x\)

\(\displaystyle -4 * 4 = -16\)

Put all of these terms together:

\(\displaystyle 2x^2 + 4x - 8x - 16\)

Combine like terms:

\(\displaystyle 2x^2 - 4x - 16\)

To simplify the polynomial, begin by multiplying the first binomial by every term within the parentheses:

\(\displaystyle ab^{-2}(a^2b+a^{-1}b^3-a^3b^{-1})\)

\(\displaystyle aa^2b^{-2}b+aa^{-1}b^{-2}b^3-aa^3b^{-2}b^{-1}\)

Now, combine like terms:

\(\displaystyle a^3b^{-1}+b^1-a^4b^{-3}\)

Convert the polynomial into fraction form:

\(\displaystyle \frac{a^3}{b}+b-\frac{a^4}{b^3}\)

To simplify the polynomial, begin by rearranging the terms to have positive exponents:

\(\displaystyle \frac{-18a^{-2}b^3c^{-4}}{12ab^{-2}c^{-3}}\)

\(\displaystyle \frac{-18b^3b^2c^{3}}{12aa^2c^{4}}\)

Now, combine like terms:

\(\displaystyle \frac{-18b^5}{12a^3c^{1}}\)

Simplify the integers:

\(\displaystyle \frac{-3b^5}{2a^3c}\)

Squaring the polynomial is equivalent to:

\(\displaystyle (5n^{3x}-2m^{x+2})^2\)

\(\displaystyle (5n^{3x}-2m^{x+2})(5n^{3x}-2m^{x+2})\)

Use the FOIL method to multiply the terms:

F - First

O - Outer

I - Inner

L - Last

\(\displaystyle 25n^{6x}-10n^{3x}m^{x+2}-10n^{3x}m^{x+2}+4m^{2x+4}\)

Combine like terms:

\(\displaystyle 25n^{6x}-20n^{3x}m^{x+2}+4m^{2x+4}\)

To simplify the polynomial, begin by rearranging the terms to have positive exponents:

\(\displaystyle (\frac{-a^{-2}b^3c^{-1}}{3a^{-4}b^{-1}c^3})^{-2}\)

\(\displaystyle (\frac{-a^{4}b^3b^1}{3a^{2}c^3c^1})^{-2}\)

Rearrange the terms once again so that the outer exponent is positive. Also, combine like terms:

\(\displaystyle (\frac{-3c^4}{a^{2}b^4})^{2}\)

Now, square the polynomial:

\(\displaystyle \frac{9c^8}{a^{4}b^8}\)

To simplify the polynomial, begin by combining the terms within the parentheses and multiplying the integers:

\(\displaystyle (5a)(6a^2b)(3ab^3)+(2a)^2(3b^3)(2a^2b)\)

\(\displaystyle 90a^4b^4+24a^4b^4\)

Now, add together like terms:

\(\displaystyle 90a^4b^4+24a^4b^4=114a^4b^4\)

To simplify the polynomial, begin by rearranging the terms to have positive exponents:

\(\displaystyle \frac{-9x^{-2}y^3z^{-1}}{3x^{-4}yz^2}\)

\(\displaystyle \frac{-9x^{4}y^3}{3x^{2}yz^2z^1}\)

Now, combine like terms:

\(\displaystyle \frac{-9x^{2}y^2}{3z^3}\)

Simplify the integers:

\(\displaystyle \frac{-3x^{2}y^2}{z^3}\)