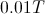We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Physics : Understanding the Relationship with Current

Study concepts, example questions & explanations for High School Physics

Create An Account

All High School Physics Resources

6 Diagnostic Tests 233 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #51 : Electricity And Magnetism

A current of $\displaystyle 8.5*10^8A$ runs through a straight wire. If the resulting magnetic field has a radius of 1.2m $\displaystyle 1.2m$, how strong is the magnetic field?

$\small \mu_0=4\pi*10^{-7}\frac{T\cdot m}{A}$ $\displaystyle \small \mu_0=4\pi*10^{-7}\frac{T\cdot m}{A}$

Possible Answers:

0.01T $\displaystyle 0.01T$

141.67T $\displaystyle 141.67T$

340T $\displaystyle 340T$

30.22T $\displaystyle 30.22T$

337.6T $\displaystyle 337.6T$

Correct answer:

141.67T $\displaystyle 141.67T$

Explanation:

Ampere's law states:

$B=\frac{\mu_0 I}{2\pi r}$ $\displaystyle B=\frac{\mu_0 I}{2\pi r}$.

In other words, the magnetic field ($\displaystyle B$), is equal to a constant ( $\mu_0$ $\displaystyle \mu_0$) times the current ($\displaystyle I$) divided by the circumference of the magnetic field it is creating.

We are given the current, the constant, and the radius. Using these values, we can solve for the magnetic field strength.

$B=\frac{\mu_0 I}{2\pi r}$ $\displaystyle B=\frac{\mu_0 I}{2\pi r}$

$B=\frac{(4\pi*10^{-7}\frac{T\cdot m}{A})( 8.5*10^8A)}{2\pi 1.2m}$ $\displaystyle B=\frac{(4\pi*10^{-7}\frac{T\cdot m}{A})( 8.5*10^8A)}{2\pi 1.2m}$

Notice that the $\pi$ $\displaystyle \pi$ cancels out.

$B=\frac{(4*10^{-7}\frac{T\cdot m}{A}) (8.5*10^8A)}{2* 1.2m}$ $\displaystyle B=\frac{(4*10^{-7}\frac{T\cdot m}{A}) (8.5*10^8A)}{2* 1.2m}$

$B=\frac{340{T\cdot m}}{2.4m}$ $\displaystyle B=\frac{340{T\cdot m}}{2.4m}$

$\displaystyle B=141.67T$

Report an Error

View Tutors

Neha
Certified Tutor

Arizona State University, Bachelor of Science, Systems Engineering.

View Tutors

Chinette
Certified Tutor

Univesity of Cagayan Valley, Bachelor in Arts, Arts, General. St Joseph College of Que zon City, Masters in Education, Specia...

View Tutors

Daniel
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Psychology.

All High School Physics Resources

6 Diagnostic Tests 233 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in San Francisco-Bay Area, ISEE Tutors in Boston, GRE Tutors in Atlanta, Algebra Tutors in Houston, GRE Tutors in New York City, ISEE Tutors in San Diego, Computer Science Tutors in Washington DC, Physics Tutors in Phoenix, Chemistry Tutors in Houston, Computer Science Tutors in Phoenix

Popular Courses & Classes

Spanish Courses & Classes in Boston, LSAT Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Chicago, GMAT Courses & Classes in San Diego, MCAT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Phoenix, SSAT Courses & Classes in Phoenix, GMAT Courses & Classes in Denver

Popular Test Prep

ISEE Test Prep in Chicago, ACT Test Prep in Washington DC, ISEE Test Prep in Los Angeles, ISEE Test Prep in Phoenix, ACT Test Prep in Houston, ISEE Test Prep in Washington DC, SAT Test Prep in Denver, GRE Test Prep in San Diego, GRE Test Prep in Philadelphia, GRE Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Physics : Understanding the Relationship with Current

Study concepts, example questions & explanations for High School Physics

All High School Physics Resources

Example Questions

Example Question #51 : Electricity And Magnetism

All High School Physics Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: