Exactitud y error
Algunos problemas matemáticos requieren de una respuesta exacta, mientras que otros, con una respuesta aproximada es suficiente.
Cuando un problema involucra la medida de una cantidad del mundo real, siempre hay un cierto nivel de aproximación que esta sucediendo. Por ejemplo, considere dos problemas diferentes que involucran medidas de tiempo. Si el problema involucra velocistas corriendo los 100 metros, necesitará usar medidas precisas: centésimas de un segundo o mejores. Si el problema involucra edades de personas, es usualmente suficiente aproximarla al año más cercano.
Algunas veces cuando un problema involucra raíces cuadradas u otros números irracionales como pi , o incluso una fracción complicada, es muy útil usar aproximaciones decimales—por lo menos al final, cuando va a dar su respuesta.
Ejemplo 1:
Deanna esta construyendo una cerca de alambre para su jardín de la forma siguiente. Encuentre la longitud de la hipotenusa del triángulo en metros.

Usando el teorema de Pitagóras, obtenemos:

Así la hipotenusa es de
![]() metros de largo. Esa es la respuesta exacta. Pero tener la respuesta en esta forma no es muy útil si estamos intentando construir algo. Como corta una pieza de alambre de
metros de largo. Esa es la respuesta exacta. Pero tener la respuesta en esta forma no es muy útil si estamos intentando construir algo. Como corta una pieza de alambre de
![]() m de largo?
m de largo?
Una buena calculadora nos dará el valor de sqrt(56) correcto para 30 lugares de decimal:
![]()
Incluso esta es una aproximación. Pero es una mucho mejor aproximación la que necesita. En este caso, redondear el valor al centímetro más cercano (centésima de un metro) es probablemente suficiente.
![]()
La exactitud de una medida o aproximación es el grado de cercanía con el valor exacto. El error es la diferencia entre la aproximación y el valor exacto.
Cuando trabaja con problemas de multipasos, debe tener cuidado con las aproximaciones. Algunas veces, un error que es aceptable en un paso puede multiplicarse en un error más grande al final.
Ejemplo 2:
Un disco de plástico es de la forma de un círculo exactamente de 11 pulgadas en diámetro. Encuentre el área combinada de 10,000 de tales discos.
Suponga que usa 3.14 como una aproximación para π. Usando la fórmula para el área de un círculo, obtenemos que el área de un disco es:

Multiplique este valor por 10,000 para obtener el área combinada de 10,000 discos.
![]()
Esto nos da una respuesta de 3,799,400 pulgadas cuadradas. Pero espere!
Vea que pasa cuando usamos un valor más exacto para π tal como 3.1416:
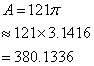
Multiplique esto por 10,000 para obtener el área combinada:
![]()
Esto es casi 2000 pulgadas cuadradas más que nuestra estimación previa!
- Arizona Bar Exam Test Prep
- Series 57 Courses & Classes
- CPPA - Certified Professional Public Adjuster Test Prep
- CLEP College Composition Modular Tutors
- Pre-Calculus for Business Tutors
- CompTIA Courses & Classes
- Missouri Bar Exam Courses & Classes
- New Mexico Bar Exam Courses & Classes
- GED Reasoning Through Language Arts Tutors
- Utah Bar Exam Test Prep
- ACT Reading Test Prep
- Oracle Certified Associate, Java SE 8 Programmer Courses & Classes
- Computer Programming Tutors
- Kindergarten Homework Tutors
- Actuarial Exam LTAM Test Prep
- ASE - National Institute for Automotive Service Excellence Training
- Washington Bar Exam Test Prep
- Technical Writing Tutors
- Minecraft Tutors
- OAT Physics Test Prep