Teorema de los ángulos alternos interiores
El Teorema de los ángulos alternos interiores establece que, cuando dos rectas paralelas se cortan por una transversal , los ángulos alternos interiores resultantes son congruentes .
Así, en la figura de abajo, si
k
||
l
, entonces
![]() 2
2

![]() 8 y
8 y
![]() 3
3

![]() 5.
5.
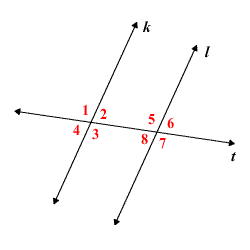
Prueba.
Ya que k || l , por el Postulado de ángulos correspondientes ,
![]() 1
1
![]()
![]() 5.
5.
Por lo tanto, por la definición de ángulos congruentes ,
m
![]() 1 =
m
1 =
m
![]() 5.
5.
Ya que
![]() 1 y
1 y
![]() 2 forman una
pareja lineal
, estos son
suplementarios
, así
2 forman una
pareja lineal
, estos son
suplementarios
, así
m
![]() 1 +
m
1 +
m
![]() 2 = 180°.
2 = 180°.
También,
![]() 5 y
5 y
![]() 8 son suplementarios, así
8 son suplementarios, así
m
![]() 5 +
m
5 +
m
![]() 8 = 180°.
8 = 180°.
Sustituyendo
m
![]() 1 por
m
1 por
m
![]() 5, obtenemos
5, obtenemos
m
![]() 1 +
m
1 +
m
![]() 8 = 180°.
8 = 180°.
Restando
m
![]() 1 en ambos lados, tenemos
1 en ambos lados, tenemos
m
![]() 8
=
180° −
m
8
=
180° −
m
![]() 1 =
m
1 =
m
![]() 2.
2.
Por lo tanto,
![]() 2
2

![]() 8.
8.
Puede probar que
![]() 3
3

![]() 5 usando el mismo método.
5 usando el mismo método.
La conversa de este teorema también es verdadera; esto es, si dos rectas k y l se cortan por una transversal de modo que los ángulos alternos interiores sean congruentes, entonces k || l .
- ARM - Associate in Risk Management Courses & Classes
- Psychology Tutors
- Observational Astronomy Tutors
- Six Sigma Courses & Classes
- API - Associate in Personal Insurance Courses & Classes
- Qualitative Research Methods Tutors
- West Virginia Bar Exam Test Prep
- Italian Renaissance Tutors
- SAT Subject Test in French with Listening Tutors
- SAT Subject Test in Biology E/M Test Prep
- Series 26 Courses & Classes
- SE Exam - Professional Licensed Engineer Structural Engineering Exam Courses & Classes
- Natural Sciences Tutors
- SHRM-SCP - Society for Human Resource Management- Senior Certified Professional Test Prep
- Animation Tutors
- CCNA Cloud - Cisco Certified Network Associate-Cloud Test Prep
- PCAT Courses & Classes
- UK GCSE Sociology Tutors
- Microbiology Tutors
- ITIL - Information Technology Infrastructure Library Training