Recta que mejor se ajusta (Método de mínimos cuadrados)

Una recta que mejor se ajusta es una línea recta que es la mejor aproximación del conjunto de datos dado.

Es usada para estudiar la naturaleza de la relación entre dos variables.

Una recta que mejor se ajusta puede ser determinada aproximadamente usando el método visual al dibujar una línea recta en una gráfica de dispersión para que tanto el número de puntos arriba de la recta y debajo de la recta sean casi iguales (y la línea pasa a tráves de tantos puntos como sea posible).

Una forma más precisa de encontrar la recta que mejor se ajusta es el método de mínimos cuadrados .

Use los pasos siguientes para encontrar la ecuación de la recta que mejor se ajusta para un conjunto de parejas ordenadas .

Paso 1: Calcule la media de los valores de x y la media de los valores de y .

Paso 2: Realice la suma de los cuadrados de los valores de x .

Paso 3: Realice la suma de cada valor de x multiplicado por su valor correspondiente y .

Paso 4: Calcule la pendiente de la recta usando la fórmula:

  

donde n es el número total de puntos de los datos.

Paso 5: Calcule la intercepción en y de la recta usando la fórmula:

donde son las medias de las coordenadas de x y y de los puntos de datos respectivamente.

Paso 6: Use la pendiente y la intercepción en y para formar la ecuación de la recta.

Solución:

Grafique los puntos en un plano coordenado .

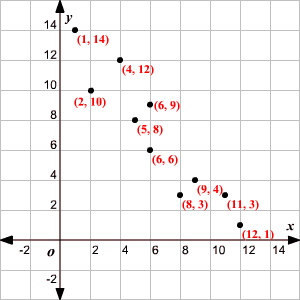
Calcule las medias de los valores de x y los valores de y , la suma de los cuadrados de los valores de x , y la suma de cada valor de x multiplicado por su valor correspondiente y .

Calcule la pendiente.

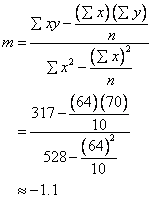
Calcule la intercepción en y .

Primero, calcule la media de los valores de x y la media de los valores de y .

Use la fórmula para calcular la intercepción en y .

Use la pendiente y la intercepción en y para formar la ecuación de la recta que mejor se ajusta.

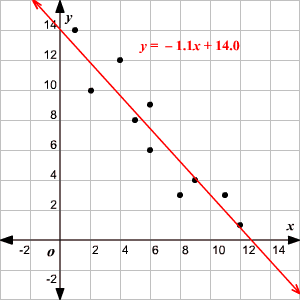
La pendiente de la recta es -1.1 y la intercepción en y es 14.0.

Por lo tanto, la ecuación es y = -1.1 x + 14.0.

Dibuje la recta en la gráfica de dispersión.