Call Now to Set Up Tutoring:

(888) 888-0446

HSPT Math : How to find the volume of a figure

Study concepts, example questions & explanations for HSPT Math

Create An Account

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Volume Of A Figure

What is the volume of a box with a length of 5, a height of 7, and a base of 16?

Possible Answers:

132

280

560

Correct answer:

560

Explanation:

When searching for the volume of a box we are looking for the amount of the space enclosed by the box. To find this we must know the formula for the volume of a box which is $Base*Height*Length=Volume\: of\: box$

Using this formula we plug in the numbers for Base, Height, and Length to get 5*7*16=560

Multiply to arrive at the answer of 560 .

Report an Error

Example Question #54 : Quadrilaterals

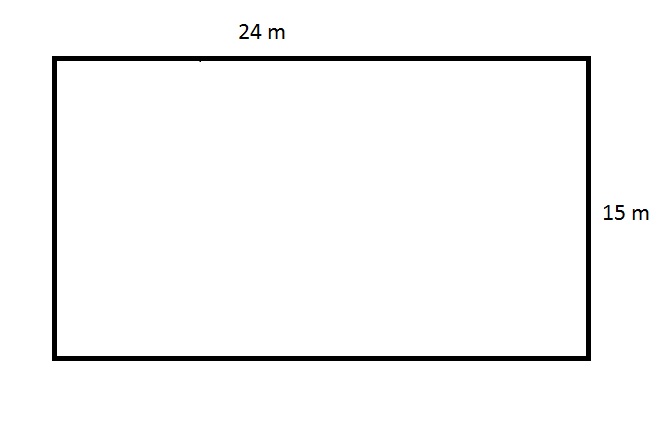
Swimming_pool

The above depicts a rectangular swimming pool for an apartment. The pool is two meters deep everywhere. What is the volume of the pool in cubic meters?

Possible Answers:

$720 \textrm{ m}^{3}$

$876\textrm{ m}^{3}$

The correct answer is not among the other choices.

$820\textrm{ m}^{3}$

$1,440\textrm{ m}^{3}$

Correct answer:

$720 \textrm{ m}^{3}$

Explanation:

The pool can be seen as a rectangular prism with dimensions 24 meters by 15 meters by 2 meters; its volume is the product of these dimensions, or

$24 \times 15 \times 2 = 720$ cubic meters.

Report an Error

Example Question #2 : How To Find The Volume Of A Figure

A cheese seller has a 2 foot x 2 foot x 2 foot block of gouda and she wants to cut it into smaller gouda cubes that are 1.5 inches on a side. How many cubes can she cut?

Possible Answers:

4096

2048

512

256

1024

Correct answer:

4096

Explanation:

First we need to determine how many of the small cubes of gouda would fit along one dimension of the large cheese block. One edge of the large block is 24 inches, so 16 smaller cubes $(24\div 1.5)$ would fit along the edge. Now we simply cube this one dimension to see how many cubes fit within the whole cube. $16^{3}=4096$ .

Report an Error

Example Question #3 : How To Find The Volume Of A Figure

An aquarium is shaped like a perfect cube; the area of each glass face is 1.44 square meters. If it is filled to the recommended 90% capacity, then, to the nearest hundred liters, how much water will it contain?

Note: 1 cubic meter = 1,000 liters.

Possible Answers:

$1,400\textup{ L}$

$1,700\textup{ L}$

$1,200\textup{ L}$

$1,600 \textup{ L}$

$1,300\textup{ L}$

Correct answer:

$1,600 \textup{ L}$

Explanation:

A perfect cube has square faces; if a face has area 1.44 square meters, then each side of each face measures the square root of this, or 1.2 meters. The volume of the tank is the cube of this, or

$1.2^{3} = 1.728$ cubic meters.

Its capacity in liters is $1.728 \times 1,000 = 1,728$ liters.

90% of this is

$1,728 \times 0.9 = 1,555.2$ liters.

This rounds to 1,600 liters, the correct response.

Report an Error

Example Question #2 : How To Find The Volume Of A Figure

Chemicals to clean a swimming pool cost $0.24 per cubic foot of water. If a pool is 6 feet deep, 14 feet long and 8 feet wide, how much does it cost to clean the pool? Round to the nearest dollar.

Possible Answers:

$\$150$

$\$161$

$\$202$

$\$672$

$\$184$

Correct answer:

$\$161$

Explanation:

The volume of the pool can be determined by multiplying the length, width, and height together.

$V = 6 \times 8 \times 14 = 672 ft^{3}$

Each cubit foot costs 24 cents, so:

$672ft^3\times \$0.24=\$161.28\approx \$161$

Report an Error

Example Question #31 : Solid Geometry

The density of gold is $16\ g/cm^3$ and the density of glass is $2\ g/cm^3$ . You have a gold cube that is $x\ cm$ in length on each side. If you want to make a glass cube that is the same weight as the gold cube, how long must each side of the glass cube be?

Possible Answers:

1.5x

2.5x

Correct answer:

Explanation:

Weight = Density * Volume

Volume of Gold Cube = side³= x³

Weight of Gold = 16 g/cm³* x³

Weight of Glass = 3/cm³ * side³

Set the weight of the gold equal to the weight of the glass and solve for the side length:

16* x³ = 2 * side³

side³ = 16/2* x³= 8 x³

Take the cube root of both sides:

side = 2x

Report an Error

Example Question #2 : How To Find The Volume Of A Figure

What is the volume of a cylinder with a diameter of 6, and a height of 5?

Possible Answers:

$180\pi$

$30\pi$

$45\pi$

$15\pi$

$90\pi$

Correct answer:

$45\pi$

Explanation:

Write the formula to find the volume of a cylinder.

$V=\pi r^2 h$

The radius is half the diameter, which is 3.

Substitute all the known dimensions into the formula.

$V=\pi( 3^2) (5)=45\pi$

Report an Error

Example Question #2 : How To Find The Volume Of A Figure

Find the volume of the cube if the face of square has a perimeter of $\textup{4 units}$ .

Possible Answers:

$64\textup{{ units}}^{3}$

$6\textup{{ units}}^{3}$

$1\textup{{ units}}^{3}$

$16\textup{{ units}}^{3}$

$8\textup{{ units}}^{3}$

Correct answer:

$1\textup{{ units}}^{3}$

Explanation:

Find the side length of the square given the square perimeter. The perimeter of a square is:

P=4s

4=4s

s=1

The side of the cube has a length of one.

Write the formula to find the volume of a cube.

V=s^3

Substitute the side length.

$V=s^3= (1)^3=1\textup{ units}^{3}$

Report an Error

Example Question #3 : How To Find The Volume Of A Figure

Swimming_pool

One cubic meter is equal to one thousand liters.

The above depicts a rectangular swimming pool for an apartment. The pool is 2.5 meters deep everywhere. How many liters of water does the pool hold?

Possible Answers:

$1,950,000\textrm{ L}$

$195,000\textrm{ L}$

$9,000,000\textrm{ L}$

$90,000\textrm{ L}$

$900,000\textrm{ L}$

Correct answer:

$900,000\textrm{ L}$

Explanation:

The pool can be seen as a rectangular prism with dimensions meters by meters by 2.5 meters; its volume in cubic meters is the product of these dimensions, which is

$24 \times 15 \times 2.5 = 900$ cubic meter.

One cubic meter is equal to one thousand liters, so multiply:

$900 \times 1,000 = 900,000$ liters of water.

Report an Error

Example Question #3 : How To Find The Volume Of A Figure

What is the volume of the rectangular prism below?

Screen shot 2015 11 05 at 12.01.48 pm

Possible Answers:

110cm^3

90cm^3

100cm^3

47cm^3

45cm^3

Correct answer:

90cm^3

Explanation:

The formula for volume of a rectangular prism is $\small v=l\times w\times h$

$\small v=9\times\2\times5$

$\small v=90cm^3$

Remember, volume is always labeled as units to the third power.

Report an Error

View Tutors

Robert
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor in Arts, English. North Carolina Central University, Master of Arts, En...

View Tutors

Joseph
Certified Tutor

Brown University, Bachelor of Science, Education.

View Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in Seattle, Computer Science Tutors in Seattle, SSAT Tutors in Atlanta, Biology Tutors in Denver, ISEE Tutors in New York City, SSAT Tutors in Philadelphia, SSAT Tutors in Los Angeles, Algebra Tutors in Seattle, SAT Tutors in Phoenix, SAT Tutors in Washington DC

Popular Courses & Classes

Spanish Courses & Classes in Chicago, GRE Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Atlanta, GMAT Courses & Classes in San Diego, MCAT Courses & Classes in Denver, SAT Courses & Classes in Miami, MCAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Miami, GMAT Courses & Classes in Atlanta, ISEE Courses & Classes in Chicago

Popular Test Prep

GMAT Test Prep in Atlanta, MCAT Test Prep in Chicago, GRE Test Prep in Boston, GMAT Test Prep in Denver, MCAT Test Prep in Denver, LSAT Test Prep in Boston, MCAT Test Prep in Phoenix, MCAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Los Angeles, ISEE Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HSPT Math : How to find the volume of a figure

Study concepts, example questions & explanations for HSPT Math

All HSPT Math Resources

Example Questions

Example Question #1 : How To Find The Volume Of A Figure

Example Question #54 : Quadrilaterals

Example Question #2 : How To Find The Volume Of A Figure

Example Question #3 : How To Find The Volume Of A Figure

Example Question #2 : How To Find The Volume Of A Figure

Example Question #31 : Solid Geometry

Example Question #2 : How To Find The Volume Of A Figure

Example Question #2 : How To Find The Volume Of A Figure

Example Question #3 : How To Find The Volume Of A Figure

Example Question #3 : How To Find The Volume Of A Figure

All HSPT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: