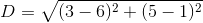ISEE Middle Level Math : Lines
Study concepts, example questions & explanations for ISEE Middle Level Math
All ISEE Middle Level Math Resources
Example Questions
Example Question #1 : Lines
Figure NOT drawn to scale.
Evaluate 
By the Segment Addition Postulate,
Example Question #3 : How To Find Length Of A Line
What is the length of a line segment with end points 
The length of a line segment can be determined using the distance formula:
Example Question #2 : Lines
What is the length of a line with endpoints 
To find the length of this line, you can subtract 
Example Question #3 : Lines
Find the length of the line segment whose endpoints are 
We can use the distance formula:
Example Question #73 : Geometry
The point 
The radius is the distance from the center of the circle to anypoint on the circle. So we can use the distance formula in order to find the radius of the circle:
Example Question #1 : How To Find Length Of A Line
The coordinates of 
A rectangle has two diagonals with the same length. So we should find the length of 
Example Question #1 : Lines
If a circle has a radius of 12 inches, the biggest line that would be drawn within the circle is:
The largest line that can be drawn within a circle is the diamater. The diameter is equal to twice the radius. Given that the radius is equal to 12 inches, the largest line that could be drawn (the diameter) would be equal to 24 inches.
Example Question #4 : How To Find Length Of A Line
If you stand on a giant number line at point 
The distance on a number line is the number of whole number places between two numbers. When you are going from a negative value to a positive one or vice versa, you must find the distance from 
Example Question #1 : Lines
One of the legs on a right triangle has a measurement of 
The Pythagorean Theorem states:
Example Question #6 : How To Find Length Of A Line
A right triangle has one leg with a length of 
The Pythagorean Theorem states that
Where 
Certified Tutor
All ISEE Middle Level Math Resources
