Pre-Algebra : Number Lines
Study concepts, example questions & explanations for Pre-Algebra
All Pre-Algebra Resources
Example Questions
Example Question #1 : Number Lines
Which of the following numbers is depicted by the point on the number line?
The point lies halfway between 
Example Question #1 : How To Plot Fractions On A Number Line
Plot the fraction 
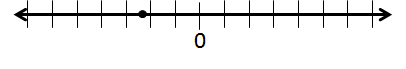
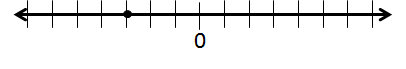
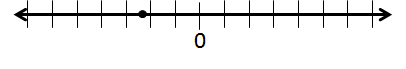
The fraction 
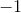
Because 
Example Question #1 : Algebra Ii
Find the distance between 
To find the distance on a number line:
Example Question #2 : Number Lines
Express this inequality statement using symbols.
Example Question #3 : Number Lines
Find the inequality that corresponds to the following number line.
When looking at the number line, we can see that x is any integer between 2 and 7.
Anything to the right of an integer is considered "greater than" and anything left of an integer is considered "less than".
So, we know that x is greater than 2, but less than 7.
Now, since the circle above the 2 is shaded in, 2 is included in the solution. The circle above the 7 is not shaded in, so 7 is not included in the solution.
We now know that x is greater than or equal to 2, and it is still less than 7.
Using the statement above, we will create 2 inequalities.
Now, 
So we have the two inequalities
We can combine them, and it'll look like this
Example Question #4 : Number Lines
Put in order from least to greatest.
Thus, in increasing order:
Example Question #3 : Number Lines
Find the inequality that corresponds with this number line.
When looking at the number line,
we see at -5 there is a filled in circle. We also see there is an arrow going to the right of -5. Every integer to the right of -5 is greater than -5 itself. Because the circle above -5 is filled in, we know -5 is included in the inequality. We get
Example Question #82 : Number Theory
Put the following numbers in order from least to greatest.
There is only one negative number in the numbers.
The next biggest is 
Next is 
Next is 
Lastly is
Certified Tutor
All Pre-Algebra Resources
