Call Now to Set Up Tutoring:

(888) 888-0446

Precalculus : Ellipses

Study concepts, example questions & explanations for Precalculus

Create An Account

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Conic Sections

Find the focal points of the conic below:

$27x^{^{2}}+16y^{^{2}}+324x-96y+684 = 0$

Possible Answers:

$\left ( 6,-3+\sqrt{11}\right ) , \left (6,-3-\sqrt{11} \right )$

$\left ( -6+\sqrt{11},3\right ),\left ( -6-\sqrt{11},3\right )$

$\left ( -6,3+\sqrt{11}\right ) , \left (-6,3-\sqrt{11} \right )$

$\left ( -6,14\right ) , \left (-6,-8 \right )$

$\left ( -6,3+\sqrt{13}\right ) , \left (-6,3-\sqrt{13} \right )$

Correct answer:

$\left ( -6,3+\sqrt{11}\right ) , \left (-6,3-\sqrt{11} \right )$

Explanation:

The first thing we want to do is put the conic (an ellipse because the x²and the y² terms have the same sign) into a better form i.e.

$\frac{\left ( x-h\right )^2}{a^2}+\frac{\left ( y-k\right )^2}{b^2}=1$

where (h,k) is the center of our ellipse.

We will continue by completing the square for both the x and y binomials.

First we seperate them into two trinomials:

$\left ( 27x^2+324x+0\right )+\left ( 16y^2-96y+0\right )=-684$

then we pull a 27 out of the first one and a 16 out of the second

$27\left ( x^2+12x+0\right )+16\left ( y^2-6y+0\right )=-684$

then we add the correct constant to each trinomial (being sure to add the same amount to the other side of our equation.

$27\left ( x^2+12x+36\right )+16\left ( y^2-6y+9\right )=-684+27(36)+16(9)$

then we factor our trinomials and divide by 16 and 27 to get

$\frac{\left ( x+6\right )^2}{16}+\frac{\left ( y-3\right )^2}{27}=1$

so the center of our ellipse is (-6,3) and we calculate the distance from the focal points to the center by the equation:

$c^2=\left | a^2-b^2\right |$

and we know that our ellipse is stretched in the y direction because b>a so our focal points will be c displaced from our center.

with $c=\sqrt{11}$

our focal points are $\left ( -6,3+\sqrt{11}\right ) , \left (-6,3-\sqrt{11} \right )$

Report an Error

Example Question #1 : Ellipses

Find the center of this ellipse:

$33x^2+13y^2-396x+26\sqrt{7}y+850=0$

Possible Answers:

$(6,\sqrt7)$

(-23,17)

(23,-17)

$(6,-\sqrt7)$

(36,7)

Correct answer:

$(6,-\sqrt7)$

Explanation:

To find the center of this ellipse we need to put it into a better form. We do this by rearranging our terms and completing the square for both our y and x terms.

$33(x^2-12x)+13(y^2+2\sqrt7y)=-850$

completing the square for both gives us this.

$33(x^2-12x+36)+13(y^2+2\sqrt7y+7)=429$

$33(x-6)^2+13(y+\sqrt7)^2=429$

we could divide by 429 but we have the information we need. The center of our ellipse is $(6,-\sqrt7 )$

Report an Error

Example Question #2 : Conic Sections

What is the equation of the elipse centered at the origin and passing through the point (5, 0) with major radius 5 and minor radius 3?

Possible Answers:

$\frac{x^2}{3} + \frac{y^2}{5} = 1$

$\frac{x^2}{9} + \frac{y^2}{25} = 1$

$\frac{x^2}{25} + \frac{y^2}{9} = 1$

$\frac{x^2}{5} + \frac{y^2}{3} = 1$

$\frac{x^2}{25} - \frac{y^2}{9} = 1$

Correct answer:

$\frac{x^2}{25} + \frac{y^2}{9} = 1$

Explanation:

The equation of an ellipse is

$\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1$ ,

where a is the horizontal radius, b is the vertical radius, and (h, k) is the center of the ellipse. In this case we are told that the center is at the origin, or (0,0), so both h and k equal 0. That brings us to:

$\frac{(x-0)^2}{a^2} + \frac{(y-0)^2}{b^2} = 1$

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

We are told about the major and minor radiuses, but the problem does not specify which one is horizontal and which one vertical. However it does tell us that the ellipse passes through the point (5, 0), which is in a horizontal line with the center, (0, 0). Therefore the horizontal radius is 5.

The vertical radius must then be 3. We can now plug these in:

$\frac{x^2}{5^2} + \frac{y^2}{3^2} = 1$

$\frac{x^2}{25} + \frac{y^2}{9} = 1$

Report an Error

Example Question #2 : Ellipses

An ellipse is centered at (-3, 2) and passes through the points (-3, 6) and (4, 2). Determine the equation of this eclipse.

Possible Answers:

$\frac{(x+3)^2}{16} + \frac{(y-2)^2}{49} = 1$

$\frac{(x+3)^2}{49} + \frac{(y-2)^2}{16} = 1$

$\frac{(x+3)^2}{7} + \frac{(y-2)^2}{4} = 1$

$\frac{(x-3)^2}{49} + \frac{(y-2)^2}{16} = 1$

$\frac{(x-3)^2}{49} + \frac{(y+2)^2}{16} = 1$

Correct answer:

$\frac{(x+3)^2}{49} + \frac{(y-2)^2}{16} = 1$

Explanation:

The usual form for an ellipse is

$\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1$ ,

where (h, k) is the center of the ellipse, a is the horizontal radius, and b is the vertical radius.

Plug in the coordinate pair:

$\frac{(x-(-3))^2}{a^2} + \frac{(y-2)^2}{b^2} = 1$

$\frac{(x+3)^2}{a^2} + \frac{(y-2)^2}{b^2} = 1$

Now we have to find the horizontal radius and the vertical radius. Let's compare points; we are told the ellipse passes through the point (-3, 6), which is vertically aligned with the center. Therefore the vertical radius is 4.

Similarly, the ellipse passes through the point (4, 2), which is horizontally aligned with the center. This means the horizontal radius must be 7.

Substitute:

$\frac{(x+3)^2}{7^2} + \frac{(y-2)^2}{4^2} = 1$

$\frac{(x+3)^2}{49} + \frac{(y-2)^2}{16} = 1$

Report an Error

Example Question #1 : Pre Calculus

What is the shape of the graph indicated by the equation?

$\frac{x^{2}}{16}+\frac{y^2}{4}=1$

Possible Answers:

Circle

Parabola

Ellipse

Hyperbola

Correct answer:

Ellipse

Explanation:

An ellipse has an equation that can be written in the format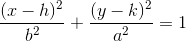 $\frac{(x-h)^2}{b^2}+\frac{(y-k)^2}{a^2}=1$ . The center is indicated by (h,k) , or in this case (0,0) .

Report an Error

View Pre-Calculus Tutors

Shane
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Computer Engineering, General.

View Pre-Calculus Tutors

Yucheng
Certified Tutor

The University of Texas at Austin, Bachelor of Science, Mechanical Engineering.

View Pre-Calculus Tutors

Yuliya
Certified Tutor

University of Maryland-College Park, Bachelor of Science, Mathematics. George Washington University, Masters in Education, Ed...

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in San Francisco-Bay Area, ACT Tutors in Philadelphia, SSAT Tutors in San Diego, Chemistry Tutors in New York City, ACT Tutors in Dallas Fort Worth, GMAT Tutors in Philadelphia, Computer Science Tutors in Philadelphia, French Tutors in Phoenix, Reading Tutors in Dallas Fort Worth, Calculus Tutors in Chicago

Popular Courses & Classes

SAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Seattle, ACT Courses & Classes in Atlanta, MCAT Courses & Classes in Houston, GMAT Courses & Classes in Washington DC, ACT Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Atlanta, Spanish Courses & Classes in Houston, MCAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

SAT Test Prep in Los Angeles, LSAT Test Prep in Atlanta, SSAT Test Prep in Miami, ACT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Seattle, ACT Test Prep in Houston, SSAT Test Prep in Denver, SAT Test Prep in Washington DC, LSAT Test Prep in Philadelphia, ISEE Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Precalculus : Ellipses

Study concepts, example questions & explanations for Precalculus

All Precalculus Resources

Example Questions

Example Question #1 : Conic Sections

Example Question #1 : Ellipses

Example Question #2 : Conic Sections

Example Question #2 : Ellipses

Example Question #1 : Pre Calculus

All Precalculus Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: