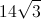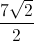All Precalculus Resources
Example Questions
Example Question #1 : Trigonometric Operations

What is the 
Example Question #2 : Trigonometric Operations

In the right triangle above, which of the following expressions gives the length of y?


Example Question #21 : Trigonometric Operations
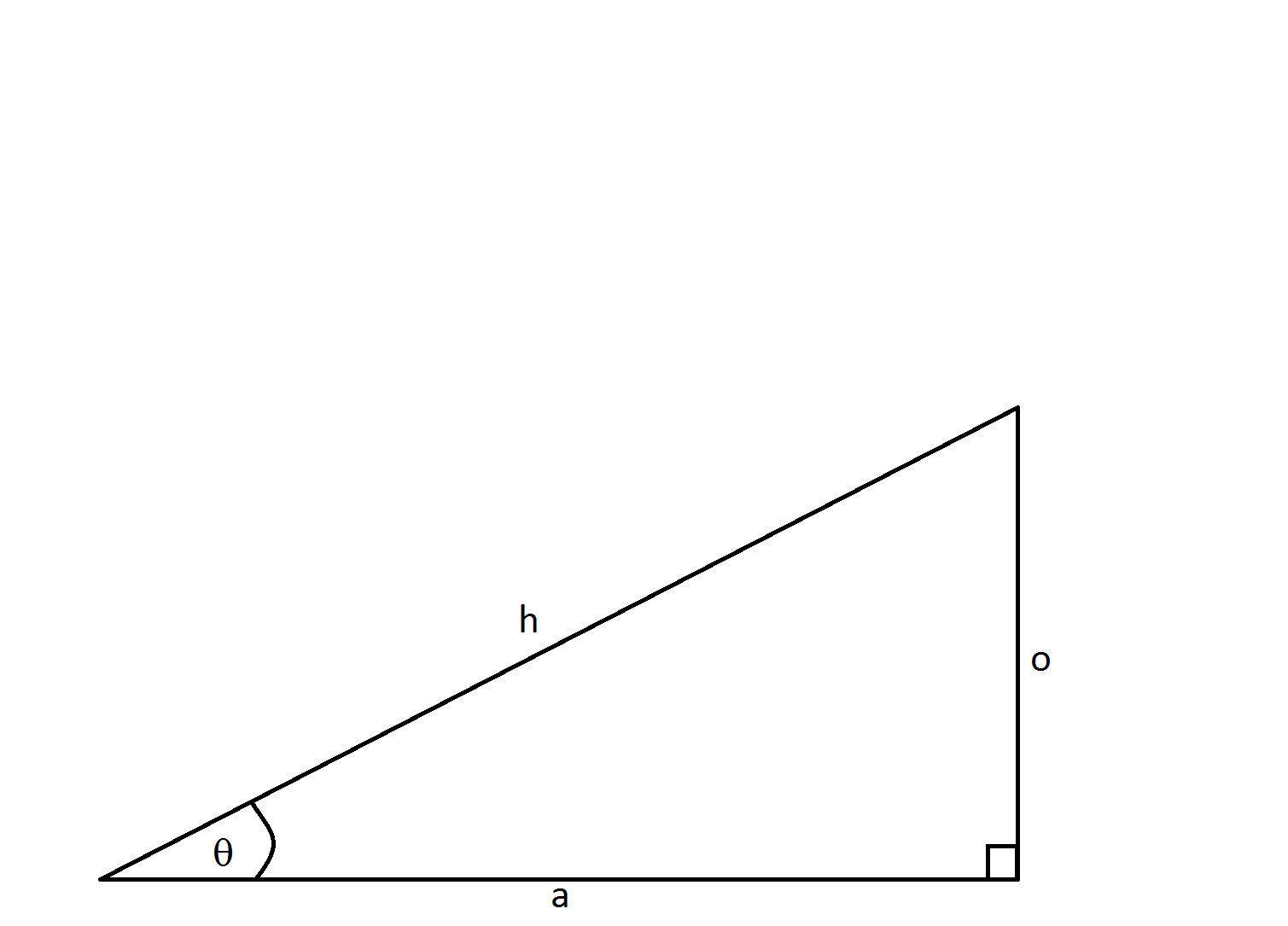
What is 


In order to find 



Now to find the measure of the angle using the 
If you calculated the angle's measure to be 
Example Question #1 : Graphing The Sine And Cosine Functions

If 




Not enough information to solve
This problem can be easily solved using trig identities. We are given the hypotenuse 



Rearrange to solve for 
If you calculated the side to equal 


Example Question #2 : Graphing The Sine And Cosine Functions

What is the length of CB?
Example Question #92 : Trigonometry

In this figure, angle 



Undefined
For this problem, use the law of sines:
%7D)
In this case, we have values that we can plug in:
Example Question #1 : Applying The Law Of Sines
 In this figure, if angle
In this figure, if angle 



(NOTE: Figure not necessarily drawn to scale.)
Undefined
First, observe that this figure is clearly not drawn to scale. Now, we can solve using the law of sines:

In this case, we have values that we can plug in:
Example Question #1 : Trigonometric Functions

In this figure, if angle 



Undefined
Since 
That means that 
In this problem, that would be:
Plug in our given values:
Example Question #63 : Pre Calculus

In this figure, 



Undefined
Notice that these sides fit the pattern of a 30:60:90 right triangle: 
In this case, 
Since angle 


Example Question #64 : Pre Calculus
A triangle has angles of 



The pattern for 

If the side opposite 



All Precalculus Resources