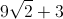PSAT Math : How to multiply square roots
Study concepts, example questions & explanations for PSAT Math
All PSAT Math Resources
Example Questions
Example Question #1 : How To Multiply Square Roots
Multiply and simplify. Assuming all integers are positive real numbers.
Multiply the coefficents outside of the radicals.
Then multiply the radicans. Simplify by checking for a perfect square.
Final answer is your leading coefficent, 
The final answer is 
Example Question #11 : Basic Squaring / Square Roots
Mulitply and simplify. Assume all integers are positive real numbers.
Order of operations, first distributing the 
The final answer is 
Example Question #1 : How To Multiply Square Roots
The square root(s) of 36 is/are ________.
-6
6 and -6
None of these answers are correct.
6, -6, and 0
6
6 and -6
To square a number is to multiply that number by itself. Because 6 x 6 = 36 AND -6 x -6 = 36, both 6 and -6 are square roots of 36.
Example Question #1 : How To Multiply Square Roots
Simplify:
Multiplication of square roots is easy! You just have to multiply their contents by each other. Just don't forget to put the result "under" a square root! Therefore:
becomes
Now, you need to simplify this:
You can "pull out" two 
After pulling out the 
Certified Tutor
All PSAT Math Resources
