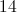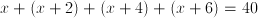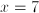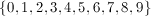All PSAT Math Resources
Example Questions
Example Question #1 : How To Find The Number Of Integers Between Two Other Integers
A custom-made ruler is 

There will be 15 gaps of 
Example Question #1 : Counting / Sets
How many prime numbers are between 1 to 25?
A prime numbers is a number greater than 1 that can only be divided by 1 and itself. Simply count from 1 to 25 and see how many values fit the criteria.
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25
Prime numbers are underlined. Nine prime numbers are in this set interval.
Example Question #1 : Counting / Sets
Four consecutive odd integers sum to 40. How many of these numbers are prime?
Let x equal the smallest of the four numbers. Therefore:
Therefore the four odd numbers are 7, 9, 11, and 13. Since all are prime except 9, three of the numbers are prime.
Example Question #1 : Counting / Sets
Find the median of this set of numbers
To find the median of a set of numbers, we must first order them from smallest to greatest.
Next, we must find the number directly in the middle, which has an equal number of numbers to the right and to the left.
Therefore, our answer is 
Example Question #1904 : Psat Mathematics
Which number completes the following series: 1, 2, 4, 8, 16, 32, 64, _?
64
16
15
128
Not enough information
128
All of the numbers in this series are 2n-1. The number that we are looking for is the eighth number. So 28–1 = 27 = 128.
Example Question #351 : Arithmetic
Alhough Danielle’s favorite flowers are tulips, she wants at least one each of three different kinds of flowers in her bouquet. Roses are twice as expensive as lilies and lilies are 25% of the price of tulips. If a rose costs $20 and Danielle only has $130, how many tulips can she buy?
4
5
2
1
3
2
She can only buy 2 tulips at $80, because if she bought 3 she wouldn’t have enough to afford the other 2 kinds of flowers. She has to spend at least 30 dollars (20 + 10) on 1 rose and 1 lily.
Example Question #1 : How To Find The Missing Number In A Set
Which of the following is not a rational number?
√2
1.75
5
0.111...
.001
√2
A rational number is a number that can be written in the form of a/b, where a and b are integers, aka a real number that can be written as a simple fraction or ratio. 4 of the 5 answer choices can be written as fractions and are thus rational.
5 = 5/1, 1.75 = 7/4, .001 = 1/1000, 0.111... = 1/9
√2 cannot be written as a fraction because it is irrational. The two most famous irrational numbers are √2 and pi.
Example Question #1907 : Psat Mathematics
Which set represents all the single-digits integers (0-9) that are either prime, a perfect square, or found in the number 68?
The prime digits are 2, 3, 5, and 7.
The perfect square digits are 0, 1, 4, and 9.
The only digits not represent in these two groups are 6 and 8, which are, coincidentally, found in the number 68.
Example Question #1 : Sets
If four different integers are selected, one from each of the following sets, what is the greater sum that these four integers could have?
W = {4, 6, 9, 10}
X = {4, 5, 8, 10}
Y = {3, 6, 7, 11}
Z = {5, 8, 10, 11}
41
40
39
42
38
38
By observing each of these sets, we can easily determine the largest number in each; however, the problem is asking for us to find the greatest possible sum if we select four different integers, one from each set. The largest number is 11. We will either select this number from set Y or set Z.
We will select set
Y for the 11
because the next larger number in set
Z is 10, which is greater than the next largest number is set Y, 7.
We can use set Z for 10.
Because the 10 has already been selected, choosing the integer from W and X should be easy because 9 is the next largest integer from set W
and
8 is the next largest integer from set X.
11 + 10 + 9 + 8 = 38
Example Question #1 : How To Find The Missing Number In A Set
A team has a win-loss ratio of 

If a team's ratio of wins to losses increases from 

Certified Tutor
Certified Tutor
All PSAT Math Resources