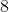Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : Absolute Value

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Absolute Value

Define an operation $\vee$ on the set of real numbers as follows:

For any two real numbers a, b

$a \vee b =| | a + 2b | + |2a + b| |$

Evaluate the expression

$4 \vee\left ( -4 \right )$

Possible Answers:

Correct answer:

Explanation:

Substitute a= 4, b = -4 in the expression:

$a \vee b =| | a + 2b | + |2a + b| |$

$4 \vee\left ( -4 \right ) =| | 4 + 2 (-4) | + |2 (4) + (-4)| |$

$4 \vee\left ( -4 \right ) =| | 4 + (-8) | + |8+ (-4)| |$

$4 \vee\left ( -4 \right ) =| | -4 | + |4| |$

$4 \vee\left ( -4 \right ) =|4+4|$

$4 \vee\left ( -4 \right ) =|8|$

$4 \vee\left ( -4 \right ) =8$

Report an Error

Example Question #1 : Absolute Value

Simplify the following expression:

$\mid -5x\mid -4+6x-\mid -3\mid$

Possible Answers:

x-1

x-7

11x-1

11x-7

Correct answer:

11x-7

Explanation:

$\mid -5x\mid -4+6x-\mid -3\mid$

To simplify, we must first simplify the absolute values.

5x -4+6x-3

Now, combine like terms:

11x-7

Report an Error

Example Question #2 : Absolute Value

Solve for .

$\left | 2x+3\right |=7$

Possible Answers:

x=-5, 2

x=5, 2

x=10,3

x=5,-2

Correct answer:

x=-5, 2

Explanation:

To solve for x we need to make two separate equations. Since it has absolute value bars around it we know that the inside can equal either 7 or -7 before the asolute value is applied.

$\left | 2x+3\right |=7$

2x +3=7 2x+3=-7

2x=4 2x=-10

x=2 x=-5

Report an Error

Example Question #1 : Absolute Value

The absolute value of a negative can be positive or negative. True or false?

Possible Answers:

True

False

Correct answer:

False

Explanation:

The absolute value of a number is the points away from zero on a number line.

Since this is a countable value, you cannot count a negative number.

This makes all absolute values positive and also make the statement above false.

Report an Error

Example Question #2 : Absolute Value

Consider the quadratic equation

$x^{2} +14 = 9x$

Which of the following absolute value equations has the same solution set?

Possible Answers:

$\left |x+ 2 \frac{1}{2} \right |= 4 \frac{1}{2}$

$\left |x- 4 \frac{1}{2} \right |= 2 \frac{1}{2}$

$\left |x+ 4 \frac{1}{2} \right |= 2 \frac{1}{2}$

$\left |x- 2 \frac{1}{2} \right |=4 \frac{1}{2}$

None of the other choices gives the correct response.

Correct answer:

$\left |x- 4 \frac{1}{2} \right |= 2 \frac{1}{2}$

Explanation:

Rewrite the quadratic equation in standard form by subtracting from both sides:

$x^{2} +14 = 9x$

$x^{2} +14 - 9x = 9x - 9x$

$x^{2}- 9x +14 = 0$

Factor this as

$(x+ \square )(x+ \square ) = 0$

where the squares represent two integers with sum and product 14. Through some trial and error, we find that and work:

(x-2)(x-7) = 0

By the Zero Product Principle, one of these factors must be equal to 0.

If x- 2= 0 then x= 2 ;

if x- 7= 0 then x= 7 .

The given equation has solution set $\left \{ 2, 7\right \}$ , so we are looking for an absolute value equation with this set as well.

This equation can take the form

|x-a| = b

This can be rewritten as the compound equation

x-a = -b x-a = b

Adding to both sides of each equation, the solution set is

x =a -b and x =a + b

Setting these numbers equal in value to the desired solutions, we get the linear system

a -b = 2

a+ b = 7

Adding and solving for :

a -b = 2

$\underline{a+ b = 7}$

= 9

$2a \div 2 = 9 \div 2$

$a = 4 \frac{1}{2}$

Backsolving to find :

a+ b = 7

$4 \frac{1}{2} + b = 7$

$4 \frac{1}{2} + b - 4 \frac{1}{2} = 7 - 4 \frac{1}{2}$

$b =2 \frac{1}{2}$

The desired absolute value equation is $\left |x- 4 \frac{1}{2} \right |= 2 \frac{1}{2}$ .

Report an Error

Example Question #6 : Absolute Value

What is the value of: $\left | -(2^{11}) \right |$ ?

Possible Answers:

2048

4096

1024

Correct answer:

2048

Explanation:

Step 1: Evaluate $2^{11}$ ...

$2^{11}=2\times2\times2\times2\times2\times2\times2\times2\times2\times2\times2=2048$

Step 2: Apply the minus sign inside the absolute value to the answer in Step 1...

$2048\rightarrow-2048$

Step 3: Define absolute value...

The absolute value of any value $\pm a$ is always positive, unless there is an extra negation outside (sometimes)..

Step 4: Evaluate...

$\left | (-2048)\right |=2048$

Report an Error

Example Question #6 : Absolute Value

Solve: $-3\left |2x+1 \right | = -3$

Possible Answers:

$\pm1$

$\textup{There is no solution.}$

-1,0

0,1

$\pm\frac{1}{2}$

Correct answer:

-1,0

Explanation:

Divide both sides by negative three.

$\frac{-3\left |2x+1 \right |}{-3} = \frac{-3}{-3}$

$\left |2x+1 \right |=1$

Since the lone absolute value is not equal to a negative, we can continue with the problem. Split the equation into its positive and negative components.

2x+1 = 1

-(2x+1) = 1

Evaluate the first equation by subtracting one on both sides, and then dividing by two on both sides.

2x+1-1= 1-1

2x=0

x=0

Evaluate the second equation by dividing a negative one on both sides.

$\frac{-(2x+1) }{-1}= \frac{1}{-1}$

2x+1 = -1

Subtract one on both sides.

2x+1 -1 = -1 -1

2x=-2

Divide by 2 on both sides.

$\frac{2x}{2}=\frac{-2}{2}$

x=-1

The answers are: -1,0

Report an Error

View SAT Subject Test in Mathematics Level 1 Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View SAT Subject Test in Mathematics Level 1 Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SAT Subject Test in Mathematics Level 1 Tutors

Samarth
Certified Tutor

Maharaja Sayajirao University of Baroda, Bachelor of Engineering, Mechanical Engineering. Concordia University-Seward, Master...

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Dallas Fort Worth, MCAT Tutors in Miami, Spanish Tutors in San Diego, Chemistry Tutors in New York City, GMAT Tutors in Washington DC, Algebra Tutors in Miami, LSAT Tutors in Chicago, Reading Tutors in San Francisco-Bay Area, SAT Tutors in Seattle, Reading Tutors in New York City

Popular Courses & Classes

SSAT Courses & Classes in San Diego, GRE Courses & Classes in Washington DC, ISEE Courses & Classes in Washington DC, SAT Courses & Classes in Houston, ACT Courses & Classes in Denver, GMAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Phoenix, LSAT Courses & Classes in Seattle, LSAT Courses & Classes in San Diego, MCAT Courses & Classes in Atlanta

Popular Test Prep

ISEE Test Prep in Houston, MCAT Test Prep in Boston, LSAT Test Prep in Seattle, ACT Test Prep in Dallas Fort Worth, SSAT Test Prep in Chicago, ACT Test Prep in Chicago, GMAT Test Prep in Dallas Fort Worth, LSAT Test Prep in Miami, MCAT Test Prep in Houston, GRE Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : Absolute Value

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #1 : Absolute Value

Example Question #1 : Absolute Value

Example Question #2 : Absolute Value

Example Question #1 : Absolute Value

Example Question #2 : Absolute Value

Example Question #6 : Absolute Value

Example Question #6 : Absolute Value

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: