In general, the formula for the area of a trapezoid is (1/2)(a + b)(h), where a and b are the lengths of the bases, and h is the length of the height. Thus, we can write the area for the trapezoid given in the problem as follows:

area of trapezoid = (1/2)(4 + s)(s)

Similarly, the area of a square with sides of length a is given by a². Thus, the area of the square given in the problem is s².

We now can set the area of the trapezoid equal to the area of the square and solve for s.

(1/2)(4 + s)(s) = s²

Multiply both sides by 2 to eliminate the 1/2.

(4 + s)(s) = 2s²

Distribute the s on the left.

4s + s² = 2s²

Subtract s² from both sides.

4s = s²

Because s must be a positive number, we can divide both sides by s.

4 = s

This means the value of s must be 4.

The answer is 4.

To solve, simply use the formula for the area of a trapezoid. Thus,

Let  be the common sidelength of the square. The area of the square is .

Construct segment . This divides the square into Rectangle  and a right triangle. The dimensions of Rectangle  are 

and

.

The area of Rectangle  s the product of these dimensions:

The lengths of the legs of Right  are

and 

The area of this right triangle is half the product of these lengths, or

This is seen below:

The sum of these areas is the area of Quadrilateral 

.

Substituting  for , the area is .

Construct  as shown in the diagram below:

Quadrilateral  is a rectangle, so opposite sides are congruent. Therefore, .

Since  is the midpoint of ,

Since  is the midpoint of , 

.

 is a right triangle, so, by the Pythagorean Theorem, 

Substituting: 

Apply the Product of Radicals and Quotient of Radicals Rules:

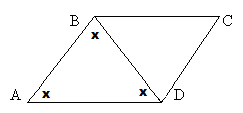
If all of the angles in triangle ABD are equal and line BD divides the parallelogram, then all angles in triangle BDC must be equal as well.

We now have two equilateral triangles, so all sides of the triangles will be equal.

All sides therefore equal 5.

5+5+5+5 = 20

To solve, simply use the formula for the area of a parallelogram. Thus,

Don't let a parallelogram fool you. It is just like a rectangle but on a slant. As long as you are given the height, and not the slant side length, you can use the same formula.

To solve, simply use the formula for the perimeter of a parallelogram. Thus,

If you don't remember this formula, you can also just sum up all the sides of the parallelogram.

Where s1 and s3 are the long sides and s2 and s4 are the short sides. Since the two pairs of sides are equal, you can sub in the following.

We have to be careful of our units. The floor is given in feet and the tile in inches. Since the floor is 6ft x 3ft. we can say it is 72in x 36in, because 12 inches equals 1 foot. If the tiles are 9in x 9in we can fit 8 tiles along the length and 4 tiles along the width. To find the total number of tiles we multiply 8 x 4 = 32. Alternately we could find the area of the floor (72 x 36, and divide by the area of the tile 9 x 9)

The dimensions for the bathroom are given in feet, but the dimensions of the tiles are given in inches; therefore, we need to convert the dimensions of the bathroom from feet to inches, because we can’t compare measurements easily unless we are using the same type of units.

Because there are twelve inches in a foot, we need to multiply the number of feet by twelve to convert from feet to inches.

10 feet = 10 x 12 inches = 120 inches

12 feet = 12 x 12 inches = 144 inches

This means that the bathroom floor is 120 inches by 144 inches. The area of Michael’s bathroom is therefore 120 x 144 in² = 17280 in².

Now, we need to find the area of the tiles in square inches and calculate how many tiles it would take to cover 17280 in².

Each tile is 4 in by 4 in, so the area of each tile is 4 x 4 in², or 16 in².

If there are 17280 in² to be covered, and each tile is 16 in², then the number of tiles we need is 17280 ÷ 16, which is 1080 tiles.

The question ultimately asks us for the cost of all these tiles; therefore, we need to multiply 1080 by 2.50, which is the price of each tile.

The total cost = 1080 x 2.50 dollars = 2700 dollars.

The answer is $2700.

Let’s say that the rectangular lot on Monday has a length of l and a width of w. The area of a rectangular is the product of the length and the width, so we can write the area of the lot on Monday as lw.

Next, we need to find an expression for the area of the lot on Tuesday. We are told that the lot is in the shape of a square and that it uses the same length of wire. If the length of the wire used is the same on both days, then the perimeter will have to remain the same. In other words, the perimeter of the square will equal the perimeter of the rectangle. The perimeter of a rectangle is given by 2l + 2w.

We also know that if s is the length of a side of a square, then the perimeter is 4s, because each side of the square is congruent. Let’s write an equation that sets the perimeter of the rectangle and the square equal.

2l + 2w = 4s

If we divide both sides by 4 and then simplify the expression, then we can write the length of the square as follows: