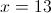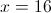Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Middle Level Math : How to find the solution to an equation

Study concepts, example questions & explanations for SSAT Middle Level Math

Create An Account

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Equations

James bought candy using a 10 dollar bill and received $\displaystyle y$ dollars in change. Which of the following describes how much James paid for the candy?

Possible Answers:

y/10 $\displaystyle y/10$

$\displaystyle y-10$

$\displaystyle 10+y$

10/y $\displaystyle 10/y$

$\displaystyle 10-y$

Correct answer:

$\displaystyle 10-y$

Explanation:

The amount of change given after a purchase is the amount the customer pays minus the cost of the item. So the cost of the item is the amount the customer pays minus the amount of change received.

Report an Error

Example Question #1 : How To Add And Subtract Fractions

For a party, Marco buys 4 boxes of cookies, each containing 10 cookies. Marco gives each of his guests 3 cookies, and then he eats 6 cookies himself. He now has 4 cookies left. How many guests did Marco give cookies to?

Possible Answers:

$\displaystyle 10$

$\displaystyle 7$

$\displaystyle 12$

$\displaystyle 11$

$\displaystyle 8$

Correct answer:

$\displaystyle 10$

Explanation:

He begins with 40 and ends with 4, so 36 cookies total were eaten. Since he ate 6 himself, that means that his guests ate 30. Since each guest ate 3 cookies, $\displaystyle 30/3 =10$ guests.

Report an Error

Example Question #1 : Ssat Middle Level Quantitative (Math)

Jacob, Judy and John add up all of their ages and get a total of 29. If they do the same thing 2 years from now, what will be their total?

Possible Answers:

$\displaystyle 40$

$\displaystyle 29$

$\displaystyle 34$

$\displaystyle 35$

$\displaystyle 31$

Correct answer:

$\displaystyle 35$

Explanation:

In two years, each person will be 2 years older. Since there are 3 of them, their ages will be $3\times2$ $\displaystyle 3\times2$ years more, so we add 6 to the original total of 29

Report an Error

Example Question #1 : Algebra

If $x\triangleright y = x- y +xy$ $\displaystyle x\triangleright y = x- y +xy$ , then $3\triangleright 2 = ?$ $\displaystyle 3\triangleright 2 = ?$

Possible Answers:

$\displaystyle 7$

$\displaystyle 2$

$\displaystyle 6$

$\displaystyle 5$

$\displaystyle 4$

Correct answer:

$\displaystyle 7$

Explanation:

Plug in 3 where you see $\displaystyle x$ and 2 where you see $\displaystyle y$ to get $3-2+3\times2$ $\displaystyle 3-2+3\times2$ . This equals 7.

Report an Error

Example Question #2 : Ssat Middle Level Quantitative (Math)

Solve for $\displaystyle x$ :

$\displaystyle 5 (x+7) = 80$

Possible Answers:

x=11 $\displaystyle x=11$

x=13 $\displaystyle x=13$

x=14 $\displaystyle x=14$

x=9 $\displaystyle x=9$

x=16 $\displaystyle x=16$

Correct answer:

x=9 $\displaystyle x=9$

Explanation:

$\displaystyle 5 (x+7) = 80$

$5 \cdot x+5 \cdot 7 = 80$ $\displaystyle 5 \cdot x+5 \cdot 7 = 80$

$\displaystyle 5x+35= 80$

$\displaystyle 5x+35 -35= 80-35$

5x= 45 $\displaystyle 5x= 45$

$5x \div 5= 45\div 5$ $\displaystyle 5x \div 5= 45\div 5$

x = 9 $\displaystyle x = 9$

Report an Error

Example Question #3 : Ssat Middle Level Quantitative (Math)

Solve for $\displaystyle n$ :

$\displaystyle 11n -35 = 97$

Possible Answers:

n = 11 $\displaystyle n = 11$

n = 12 $\displaystyle n = 12$

n = 13 $\displaystyle n = 13$

n = 9 $\displaystyle n = 9$

n = 14 $\displaystyle n = 14$

Correct answer:

n = 12 $\displaystyle n = 12$

Explanation:

Add 35, then divide by 11:

$\displaystyle 11n -35 = 97$

$\displaystyle 11n -35 +35 = 97 +35$

$\displaystyle 11n = 132$

$11n \div 11= 132\div 11$ $\displaystyle 11n \div 11= 132\div 11$

n = 12 $\displaystyle n = 12$

Report an Error

Example Question #4 : How To Find The Solution To An Equation

Solve for $\displaystyle n$ :

$\displaystyle 9n - 13 = 59$

Possible Answers:

n = 9 $\displaystyle n = 9$

n = 5 $\displaystyle n = 5$

n = 8 $\displaystyle n = 8$

n = 7 $\displaystyle n = 7$

n = 6 $\displaystyle n = 6$

Correct answer:

n = 8 $\displaystyle n = 8$

Explanation:

Add 13, then divide by 9:

$\displaystyle 9n - 13 = 59$

$\displaystyle 9n - 13 +13 = 59+13$

9n = 72 $\displaystyle 9n = 72$

$9n \div 9 = 72 \div 9$ $\displaystyle 9n \div 9 = 72 \div 9$

n = 8 $\displaystyle n = 8$

Report an Error

Example Question #3 : Equations

Solve for $\displaystyle n$ :

$\displaystyle 7n - 25 = 52$

Possible Answers:

n=12 $\displaystyle n=12$

n=14 $\displaystyle n=14$

n=13 $\displaystyle n=13$

n=11 $\displaystyle n=11$

n=15 $\displaystyle n=15$

Correct answer:

n=11 $\displaystyle n=11$

Explanation:

Add 25, then divide by 7:

$\displaystyle 7n - 25 = 52$

$\displaystyle 7n - 25 +25 = 52+25$

7n = 77 $\displaystyle 7n = 77$

$7n \div 7= 77 \div 7$ $\displaystyle 7n \div 7= 77 \div 7$

n=11 $\displaystyle n=11$

Report an Error

Example Question #5 : How To Find The Solution To An Equation

If $\displaystyle 13 < M < 17$ and $\displaystyle M$ is an even whole number, then $\displaystyle M$ could be

Possible Answers:

$\displaystyle 12$

$\displaystyle 16$

$\displaystyle 17$

$\displaystyle 13$

$\displaystyle 15$

Correct answer:

$\displaystyle 16$

Explanation:

The greater than and less than symbols describe a number that is greater than but not equal to 13 and less than but not equal to 17. The whole numbers between 13 and 17 are 14, 15, and 16. The question also qualifies that the number needs to be even so we are looking for 14 or 16. Only 16 is an answer choice available.

Report an Error

Example Question #4 : Ssat Middle Level Quantitative (Math)

$(9-4) \cdot 3 = 5 + \blacksquare$ ,

then $\blacksquare$ $\displaystyle \blacksquare$ =

Possible Answers:

$\displaystyle 6$

$\displaystyle 4$

$\displaystyle -8$

$\displaystyle 9$

$\displaystyle 10$

Correct answer:

$\displaystyle 10$

Explanation:

So order of operations says to do what's in the parentheses first. Thus

9-4=5 $\displaystyle 9-4=5$

$5 \times 3 = 15$ $\displaystyle 5 \times 3 = 15$

Thus the left side of the equation is 15. Subtract 5 from both sides to determine what the $\blacksquare$ $\displaystyle \blacksquare$ is.

$\displaystyle 15 - 5 = 10$ .

Report an Error

View SSAT- Middle Level Tutors

Gabby
Certified Tutor

University of Oregon, Bachelor in Arts, Journalism. University of Oregon, Current Grad Student, Communication, General.

View SSAT- Middle Level Tutors

Meredith
Certified Tutor

University of Arkansas at Little Rock, Bachelor in Arts, English. University of Arkansas at Little Rock, Masters in Education...

View SSAT- Middle Level Tutors

Ingrid
Certified Tutor

Northern Illinois University, Bachelor of Science, Elementary Education. Northern Illinois University, Master of Science, Cur...

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Philadelphia, Chemistry Tutors in Philadelphia, Reading Tutors in Washington DC, French Tutors in Houston, Statistics Tutors in Dallas Fort Worth, GMAT Tutors in Dallas Fort Worth, Biology Tutors in Atlanta, ISEE Tutors in Dallas Fort Worth, Statistics Tutors in San Francisco-Bay Area, Math Tutors in Chicago

Popular Courses & Classes

Spanish Courses & Classes in Seattle, SSAT Courses & Classes in Denver, GMAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Los Angeles, GMAT Courses & Classes in Seattle, MCAT Courses & Classes in Miami, Spanish Courses & Classes in Philadelphia, LSAT Courses & Classes in Seattle, ISEE Courses & Classes in Seattle, ISEE Courses & Classes in Chicago

Popular Test Prep

MCAT Test Prep in New York City, GRE Test Prep in Chicago, GRE Test Prep in Los Angeles, ISEE Test Prep in Miami, LSAT Test Prep in San Diego, LSAT Test Prep in Seattle, GRE Test Prep in New York City, ACT Test Prep in Dallas Fort Worth, GRE Test Prep in Dallas Fort Worth, ISEE Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Middle Level Math : How to find the solution to an equation

Study concepts, example questions & explanations for SSAT Middle Level Math

All SSAT Middle Level Math Resources

Example Questions

Example Question #1 : Equations

Example Question #1 : How To Add And Subtract Fractions

Example Question #1 : Ssat Middle Level Quantitative (Math)

Example Question #1 : Algebra

Example Question #2 : Ssat Middle Level Quantitative (Math)

Example Question #3 : Ssat Middle Level Quantitative (Math)

Example Question #4 : How To Find The Solution To An Equation

Example Question #3 : Equations

Example Question #5 : How To Find The Solution To An Equation

Example Question #4 : Ssat Middle Level Quantitative (Math)

All SSAT Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: