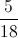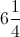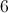Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : How to find a complex fraction

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find A Complex Fraction

Simplify:

$\frac{\frac{2}{3} + \frac{1}{5}}{\frac{4}{5}}$

Possible Answers:

$\frac{52}{75}$

$\frac{13}{12}$

$\frac{3}{7}$

$\frac{3}{10}$

$\frac{1}{5}$

Correct answer:

$\frac{13}{12}$

Explanation:

Add the fractions in the numerator, then divide the sum by the denominator:

$\frac{\frac{2}{3} + \frac{1}{5}}{\frac{4}{5}}$

$=\frac{\frac{2\cdot 5}{3\cdot 5} + \frac{1\cdot 3}{5\cdot 3}}{\frac{4}{5}}$

$=\frac{\frac{10}{15} + \frac{3}{15}}{\frac{4}{5}}$

$=\frac{\frac{10+3}{15} }{\frac{4}{5}} = \frac{\frac{13}{15} }{\frac{4}{5}}$

$= \frac{13}{15} \div \frac{4}{5} = \frac{13}{15} \times \frac{5}{4} = \frac{13}{3} \times \frac{1}{4} =\frac{13}{12}$

Report an Error

Example Question #2 : How To Find A Complex Fraction

Simplify:

$\frac{\frac{1}{3} + \frac{3}{10}}{\frac{9}{10}}$

Possible Answers:

$\frac{19}{27}$

$\frac{2}{3}$

$\frac{40}{117}$

$\frac{57}{100}$

$\frac{1}{27}$

Correct answer:

$\frac{19}{27}$

Explanation:

Simplify the sum in the numerator, then divide by the denominator:

$\frac{\frac{1}{3} + \frac{3}{10}}{\frac{9}{10}}$

$=\frac{\frac{1\cdot 10}{3 \cdot 10} + \frac{3 \cdot 3}{10 \cdot 3}}{\frac{9}{10}}$

$=\frac{\frac{10}{30} + \frac{9}{30}}{\frac{9}{10}}$

$=\frac{\frac{10+9}{30} }{\frac{9}{10}} = \frac{\frac{19}{30} }{\frac{9}{10}}$

$\frac{19}{30} \div \frac{9}{10} = \frac{19}{30}\times \frac{10}{9} = \frac{19}{3}\times \frac{1}{9} = \frac{19}{27}$

Report an Error

Example Question #3 : How To Find A Complex Fraction

Simplify:

$\frac{1\frac{1}{3}}{4 \frac{4}{5}}$

Possible Answers:

$\frac{1}{4}$

$\frac{4}{15}$

$\frac{2}{5}$

$\frac{5}{18}$

$\frac{3}{5}$

Correct answer:

$\frac{5}{18}$

Explanation:

Rewrite this as a division problem, then solve:

$\frac{1\frac{1}{3}}{4 \frac{4}{5}} = 1\frac{1}{3} \div 4 \frac{4}{5} = \frac{4}{3} \div \frac{24}{5}= \frac{4}{3} \times \frac{5}{24}= \frac{1}{3} \times \frac{5}{6}= \frac{5}{18}$

Report an Error

Example Question #4 : How To Find A Complex Fraction

Simplify:

$\frac{5}{1\frac{1}{4}}$

Possible Answers:

$6\frac{1}{4}$

$3 \frac{3}{4}$

$4 \frac{1}{2}$

Correct answer:

Explanation:

Rewrite this as a division problem, then solve:

$\frac{5}{1\frac{1}{4}} = 5 \div 1\frac{1}{4}= \frac{5}{1}\div \frac{5}{4} = \frac{5}{1}\times \frac{4}{5}= \frac{1}{1}\times \frac{4}{1} = 4$

Report an Error

Example Question #74 : Fractions

Simplify:

$\frac{3\frac{4}{5}}{3\frac{1}{2}+2\frac{1}{5}}$

Possible Answers:

$\frac{5}{9}$

$\frac{3}{4}$

$\frac{7}{10}$

$\frac{2}{3}$

$\frac{5}{8}$

Correct answer:

$\frac{2}{3}$

Explanation:

$\frac{3\frac{4}{5}}{3\frac{1}{2}+2\frac{1}{5}}$

$=3\frac{4}{5} \div \left ( 3\frac{1}{2}+2\frac{1}{5} \right )$

$= \frac{19}{5} \div \left ( \frac{7}{2}+ \frac{11}{5} \right )$

$=\frac{19}{5} \div \left ( \frac{35}{10}+ \frac{22}{10} \right )$

$=\frac{19}{5} \div \frac{57}{10}$

$=\frac{19}{5} \times \frac{10}{57}$

$=\frac{1 }{1} \times \frac{2}{3} = \frac{2}{3}$

Report an Error

Example Question #6 : How To Find A Complex Fraction

Simplify:

$\frac{3\frac{1}{2}-2\frac{1}{5}}{4\frac{3}{4}}$

Possible Answers:

$\frac{7}{25}$

$\frac{27}{100}$

$\frac{5}{19}$

The correct answer is not given among the other responses.

$\frac{9}{23}$

Correct answer:

The correct answer is not given among the other responses.

Explanation:

$\frac{3\frac{1}{2}-2\frac{1}{5}}{4\frac{3}{4}}$

$=\left ( 3\frac{1}{2}-2\frac{1}{5} \right )\div 4\frac{3}{4}}$

$= \left ( \frac{7}{2}- \frac{11}{5} \right ) \div \frac{19}{4}$

$= \left ( \frac{35}{10}- \frac{22}{10} \right ) \times \frac{4}{19}$

$= \frac{13}{10} \times \frac{4}{19}$

$= \frac{13}{5} \times \frac{2}{19}$

$= \frac{26}{95}$

This is not among the given responses.

Report an Error

Example Question #81 : Fractions

Simplify:

$\frac{3\frac{1}{2}+2\frac{1}{5}}{4\frac{3}{4}}$

Possible Answers:

$1\frac{1}{4}$

$1\frac{3}{5}$

$1\frac{1}{5}$

$1\frac{1}{6}$

$1\frac{2}{5}$

Correct answer:

$1\frac{1}{5}$

Explanation:

$\frac{3\frac{1}{2}+2\frac{1}{5}}{4\frac{3}{4}}$

$=\left ( 3\frac{1}{2}+2\frac{1}{5} \right )\div 4\frac{3}{4}}$

$= \left ( \frac{7}{2}+ \frac{11}{5} \right ) \div \frac{19}{4}$

$= \left ( \frac{35}{10}+ \frac{22}{10} \right ) \times \frac{4}{19}$

$= \frac{57}{10} \times \frac{4}{19}$

$= \frac{3}{5} \times \frac{2}{1}$

$= \frac{6}{5} = 1\frac{1}{5}$

Report an Error

Example Question #81 : Rational Numbers

Simplify, writing as a proper fraction.

$\frac{2\tfrac{1}{4}}{5\tfrac{2}{5}}$

Possible Answers:

$\frac{5}{9}$

$\frac{3}{10}$

$\frac{2}{5}$

$\frac{5}{12}$

$\frac{7}{12}$

Correct answer:

$\frac{5}{12}$

Explanation:

Remember that that fraction bar is just a division symbol. Rewrite as a division, rewrite those mixed fractions as improper fractions, then rewrite as as a multiplication by the reciprocal of the second fraction.

$\frac{2\tfrac{1}{4}}{5\tfrac{2}{5}} = 2\tfrac{1}{4} \div 5\tfrac{2}{5} = \frac{9}{4} \div \frac{27}{5} = \frac{9}{4} \cdot \frac{5}{27} = \frac{1}{4} \cdot \frac{5}{3}= \frac{5}{12}$

Report an Error

View SSAT- Upper Level Tutors

Laura Jeanne
Certified Tutor

Texas Tech University, Bachelor in Arts, Music Teacher Education. Asbury Theological Seminary, Master of Divinity, Music Teac...

View SSAT- Upper Level Tutors

Keith
Certified Tutor

Xavier University, Bachelor in Business Administration, Accounting. Ohio University-Main Campus, Masters in Education, Mathem...

View SSAT- Upper Level Tutors

Zander
Certified Tutor

Rowan-Cabarrus Community College, Associate in Arts, General Studies. North Carolina State University at Raleigh, Bachelor of...

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in Washington DC, LSAT Tutors in Phoenix, Statistics Tutors in Philadelphia, ISEE Tutors in Houston, Spanish Tutors in Boston, Calculus Tutors in New York City, English Tutors in San Diego, Reading Tutors in Boston, Statistics Tutors in Phoenix, Biology Tutors in San Francisco-Bay Area

Popular Courses & Classes

Spanish Courses & Classes in Boston, ISEE Courses & Classes in Seattle, GRE Courses & Classes in Atlanta, SAT Courses & Classes in Phoenix, Spanish Courses & Classes in Seattle, ISEE Courses & Classes in Washington DC, SSAT Courses & Classes in Phoenix, GMAT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Chicago, ACT Courses & Classes in Atlanta

Popular Test Prep

GMAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Denver, LSAT Test Prep in Los Angeles, SSAT Test Prep in New York City, MCAT Test Prep in Philadelphia, SSAT Test Prep in Atlanta, GMAT Test Prep in San Diego, SSAT Test Prep in Chicago, ISEE Test Prep in Washington DC, SSAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : How to find a complex fraction

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #1 : How To Find A Complex Fraction

Example Question #2 : How To Find A Complex Fraction

Example Question #3 : How To Find A Complex Fraction

Example Question #4 : How To Find A Complex Fraction

Example Question #74 : Fractions

Example Question #6 : How To Find A Complex Fraction

Example Question #81 : Fractions

Example Question #81 : Rational Numbers

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: