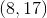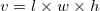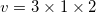The power of \(\displaystyle 10\) tells us how to move our decimal. Because we have a positive \(\displaystyle 7\) power, we move our decimal over \(\displaystyle 7\) places to the right. 

\(\displaystyle 6.\rightarrow 60000000.\)

When we have numbers that include decimals, the tenths place is always the first number to the right of the decimal, the hundredths place is to the right of the tenths place, and the thousandths place is to the right of the hundredths place. See the diagram below:

For the number in the problem:

 \(\displaystyle 564.391\)

The \(\displaystyle 9\) is in the hundredths position. 

When we write a number in expanded form, we multiply each digit by its place value. 

\(\displaystyle 2\) is in the ones place, so we multiply by \(\displaystyle 1\). 

\(\displaystyle 2\times1=2\)

\(\displaystyle 3\) is in the tenths place, so we multiply by \(\displaystyle \frac{1}{10}\). 

\(\displaystyle 3\times\frac{1}{10}=.3\)

\(\displaystyle 7\) is in the hundredths place, so we multiply by \(\displaystyle \frac{1}{100}\).

\(\displaystyle 7\times\frac{1}{100}=.07\)

Then we add the products together to check our answer: 

\(\displaystyle \frac{\begin{array}[b]{r}2.00\\ +\ .30\\ .07 \end{array}}{ \ \ \space2.37}\)

Thus, the correct answer is: 

\(\displaystyle 2\times1+3\times\left(\frac{1}{10}\right)+7\times\left(\frac{1}{100}\right)\)

When we multiply fractions, we multiply the numerator by the numerator and the denominator by the denominator. 

\(\displaystyle \frac{5}{9}\times \frac{6}{13}=\frac{30}{117}\)

\(\displaystyle \frac{30}{117}\) can be reduced to \(\displaystyle \frac{10}{39}\) by dividing both sides by \(\displaystyle 3\). 

\(\displaystyle \frac{30}{117}\frac{\div}{\div}\frac{3}{3}=\frac{10}{39}\)

\(\displaystyle 2\times (50-25)\div5\)

When solving this problem, remember order of operations PEMDAS. The parentheses come first, followed by the multiplication, and then the division.

\(\displaystyle 50-25=25\)

\(\displaystyle 25\times2=50\)

\(\displaystyle 50\div5=10\) 

When we multiply a fraction by a whole number, we first want to make the whole number into a fraction. We do that by putting the whole number over \(\displaystyle \small 1.\) Then we multiply like normal. 

\(\displaystyle \small \frac{3}{1}\times\frac{1}{2}=\frac{3}{2}\)

\(\displaystyle \small \frac{3}{2}=1\frac{1}{2}\) Because \(\displaystyle 2\) can go into \(\displaystyle \small 3\) only \(\displaystyle \small 1\) time and \(\displaystyle \small \frac{1}2{}\) is left over. 

Matt collected \(\displaystyle \small 1\frac{1}2{}\) bags of leaves. 

\(\displaystyle 3\times2+(10-8)\)

When solving this problem, remember order of operations PEMDAS. The parentheses come first followed by the multiplication, and then the addition. 

\(\displaystyle 10-8=2\)

\(\displaystyle 3\times2=6\)

\(\displaystyle 6+2=8\)

To find the location on a coordinate plane we first look at the \(\displaystyle x\)-axis, which runs horizontal and then the \(\displaystyle y\)-axis, which runs vertical. We write the point on the \(\displaystyle x\)-axis first, followed by the point on the \(\displaystyle y\)-axis. \(\displaystyle (x,y)\)

The red circle is over \(\displaystyle 30\) on the \(\displaystyle x\)-axis and up \(\displaystyle 6\) on the \(\displaystyle y\)-axis. 

The correct answer is \(\displaystyle (30,6)\)

To solve this problem we can make proportions.

We know that \(\displaystyle 1\ centimeter= .01\ meters\) and we can use \(\displaystyle x\) as our unknown. 

\(\displaystyle \frac{1\ centimeter}{.01\ meter}=\frac{x\ centimeters}{5\ meters}\)

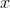
Next, we want to cross multiply and divide to isolate the  on one side. 

\(\displaystyle 1\ centimeter\times 5\ meters=.01\ meter\times x\ centimeters\)

\(\displaystyle \frac{1\ centimeter\times 5\ meters}{.01\ meter}= x\ centimeters\)

The \(\displaystyle meters\) will cancel and we are left with \(\displaystyle 500\ centimeters\)

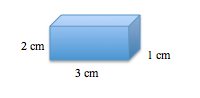
The formula for volume of a rectangular prism is \(\displaystyle \small v=l\times w\times h\)

We can use this formula and plug in the value from the question:

\(\displaystyle \small v=3\times1\times2\)

\(\displaystyle \small v=6cm^3\)

Remember, volume is always labeled as units to the third power.