All ACT Math Resources
Example Questions
Example Question #1 : Decimals With Fractions
When 5/11 is written as a decimal, what is the 100th digit to the right of the decimal point?
1
2
5
0
4
5
When 5 is divided by 11, the decimal is 0.45 repeating, with a 5 in the hundreths place. The key here is to recognize that 100 is an even number, and the 5 in 0.45 is two places to the right of the decimal point (2 also being an even number).
Example Question #202 : Fractions
Find the sum of the following:
To get the decimal from a fraction, divide the numerator by the denominator
Example Question #1 : Decimals
Find the sum to the nearest hundredth:
1. Convert the fractions to decimals by division:
2. Add the corresponding whole numbers to the decimals:
3. Add the two decimals:
Example Question #261 : Arithmetic
If 
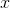
None of the other answer choices are correct
Convert all of the fractions to decimals. Thus, x is contained within the range of 0.33 < x < 0.76. The answers choices become 1/4 = 0.25, 4/12 = 0.33, 2/5 = 0.4, and 5/16 = 0.3125, respectively. Therefore, the only answer which is within the desired range is 2/5.
Example Question #262 : Arithmetic
Simplify:
Begin by multiplying all of your decimal fractions by 
Simplify:
Now perform the multiplication:
The easiest thing to do next is to subtract 

Next, convert 

Now, the common denominator can be 
Simplify:
Example Question #1331 : Act Math
Convert 0.825 into a fraction.
0.825 in fraction form is 

Example Question #261 : Arithmetic
What is 
We need to convert 
To do this, write down
Now, because the decimal goes to the hundreth place, multiply the numerator and denominator of the fraction by 100.
Now, simplify the fraction.
Example Question #1 : How To Find The Fractional Equivalent Of A Decimal
A tub of food contains 


To begin with, it is easiest just to add these decimals together using your calculator:
Now, this is the same thing as:
We can rewrite this:
To find this, you need to give the two numbers a common denominator:
This is your answer.
Example Question #263 : Arithmetic
What is the fractional equivalent of 
In decimal form 
This is equal to

This fraction cannot be reduced any further therefore it is in its final answer form.
Example Question #1 : How To Find The Fractional Equivalent Of A Decimal
Write 0.45 as a fraction.
.45 is equivalent to 45 out of 100, or 
Divide both the numerator and denominator by 5 to simplify the fraction:
All ACT Math Resources











































































