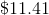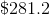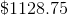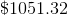The formula for compound interest is

\(\displaystyle A = P\left ( 1 + \frac{r}{n}\right )^{nt}\)

where P is the principal (original) amount, r is the interest rate (in decimal form), n is the number of times per year the interest compounds, t is the time in years, and A is the final amount.

In this problem, we are solving for time, t. The given variables from the problem are:

\(\displaystyle P = 2500\)

\(\displaystyle r = 0.031\)

\(\displaystyle n = 12\)

\(\displaystyle A = 3500\)

Plugging these into the equation above, we get

\(\displaystyle 3500 = 2500\left ( 1 + \frac{0.031}{12}\right )^{12t}\)

This simplifies to

\(\displaystyle 1.4 = \left ( 1 + \frac{0.031}{12}\right )^{12t}\)

We can solve this by taking the natural log of both sides

\(\displaystyle \ln \left (1.4 \right ) = \ln \left (\left ( 1 + \frac{0.031}{12}\right )^{12t} \right )\)

\(\displaystyle \ln \left (1.4 \right ) = 12t\ln \left ( 1 + \frac{0.031}{12}\right )\)

\(\displaystyle \frac{\ln \left (1.4 \right ) }{\ln \left (1 + \frac{0.031}{12}\right ) }= 12t\)

\(\displaystyle \frac{\ln \left (1.4 \right ) }{12\ln \left (1 + \frac{0.031}{12}\right ) }= t\)

\(\displaystyle t = 10.86 \approx 11\)

The formula for compound interest is

\(\displaystyle A = P\left ( 1 + \frac{r}{n}\right )^{nt}\)

where P is the principal (original) amount, r is the interest rate (in decimal form), n is the number of times per year the interest compounds, t is the time in years, and A is the final amount.

In this problem, we are solving for the principal, P. The given variables from the problem are:

\(\displaystyle r = 0.047\)

\(\displaystyle n = 4\)

\(\displaystyle t = 5\)

\(\displaystyle A = 3600\)

Plugging these into the equation above, we get

\(\displaystyle 3600 = P\left ( 1 + \frac{0.047}{4}\right )^{4\cdot 5}\)

Solving for P, we get

\(\displaystyle 3600 = P\left ( 1.01175)^{20}\)

\(\displaystyle \frac{3600}{(1.01175)^{20}}} = P\)

\(\displaystyle 2850 = P\)

Each year, you can calculate your interest by multiplying the principle (\(\displaystyle \$5000\)) by \(\displaystyle 1.025\). For one year, this would be:

\(\displaystyle 1.025*5000=5125\)

For two years, it would be:

\(\displaystyle 5125*1.025\), which is the same as \(\displaystyle 1.025*1.025*5000\)

Therefore, you can solve for a five year period by doing:

\(\displaystyle 1.025^5*5000\)

Using your calculator, you can expand the \(\displaystyle 1.025^5\) into a series of multiplications. This gives you \(\displaystyle 5657.041064453125\), which is closest to \(\displaystyle \$5657\). 

It is easiest to break this down into steps. For each year, you will multiply by \(\displaystyle 1.035\) to calculate the new value. Therefore, let's make a chart:

After year 1: \(\displaystyle 7500*1.035=7762.5\); Total interest: \(\displaystyle 262.5\)

After year 2: \(\displaystyle 7762.5*1.035=8034.1875\); Let us round this to \(\displaystyle 8034.19\); Total interest: \(\displaystyle 271.69\)

After year 3: \(\displaystyle 8034.19 * 1.035 = 8315.38665\); Let us round this to \(\displaystyle 8315.39\); Total interest: \(\displaystyle 281.2\)

Thus, the positive difference of the interest from the last period and the interest from the first period is: \(\displaystyle 281.2-271.69=9.51\)

Recall that the equation for compounded interest (with annual compounding) is:

\(\displaystyle b_n_e_w=b_i_n_i_t_i_a_l*(1 + r)^t\)

Where \(\displaystyle b\) is the balance, \(\displaystyle r\) is the rate of interest, and \(\displaystyle t\) is the number of years.

Thus, for our data, we need to know:

\(\displaystyle b_n_e_w=2000 * (1 + 0.04)^1^0=2000 * (1.04)^1^0\)

This is approximately \(\displaystyle \$2960.49\).

Recall that the equation for compounded interest (with annual compounding) is:

\(\displaystyle b_n_e_w=b_i_n_i_t_i_a_l*(1 + r)^t\)

Where \(\displaystyle b\) is the balance, \(\displaystyle r\) is the rate of interest, and \(\displaystyle t\) is the number of years.

Thus, for our data, we need to know:

\(\displaystyle b_n_e_w=4500 * (1 + 0.055)^5=4500 * (1.055)^5\)

This is approximately \(\displaystyle \$5881.32\).

Recall that the equation for compounded interest (with quarterly compounding) is:

\(\displaystyle b_n_e_w=b_i_n_i_t_i_a_l*(1 + \frac{r}{n})^t^n\)

Where \(\displaystyle b\) is the balance, \(\displaystyle r\) is the rate of interest, \(\displaystyle t\) is the number of years, and \(\displaystyle n\) is the number of times it is compounded per year.

Thus, for our data, we need to know:

\(\displaystyle b_n_e_w=12000 * (1 + \frac{0.08}{4})^4^*^4=12000 * (1.02)^1^6\)

This is approximately \(\displaystyle \$16473.43\).

Recall that the equation for compounded interest (with annual compounding) is:

\(\displaystyle b_n_e_w=b_i_n_i_t_i_a_l*(1 + r)^t\)

Where \(\displaystyle b\) is the balance, \(\displaystyle r\) is the rate of interest, and \(\displaystyle t\) is the number of years.

Thus, for our data, we need to know:

\(\displaystyle 10451.43=4500 * (1 + x)^2^0\)

Now, let's use \(\displaystyle b\) for \(\displaystyle 1+x\). This gives us:

\(\displaystyle 10451.43=4500 * (b)^2^0\)

Using a logarithm, this can be rewritten:

\(\displaystyle log_b(\frac{10451.43}{4500})=20\)

This can be rewritten:

\(\displaystyle \frac{log(2.32254)}{log(b)}=20\)

Now, you can solve for \(\displaystyle log(b)\):

\(\displaystyle \frac{1}{log(b)}=\frac{20}{log(2.32254)}\)

or

\(\displaystyle log(b)=\frac{log(2.32254)}{20}\)

Now, finally you can rewrite this as:

\(\displaystyle 10^\frac{log(2.32254)}{20}=b\)

Thus, \(\displaystyle b=1.04303326670287....\)

Now, round this to \(\displaystyle 1.0430\) and recall that \(\displaystyle b=1 + x\)

Thus, \(\displaystyle 1+x = 1.0430\) and \(\displaystyle x = 0.043\) or \(\displaystyle 4.3\%\)

First, break the problem into two segments: the amount Jack invests in the high-yield savings, and the amount Jack invests in the simple interest account (10,000 and 5,000 respectively).

Now let's work with the high-yield savings account. $10,000 is invested at an annual rate of 8%, compounded quarterly. We can use the compound interest formula to solve:

\(\displaystyle \text{Final Balance}=\text{ Principal} \cdot \bigg(1+\frac{\text{Interest Rate}}{c}\bigg)^{(\text{Time})(c)}\)

Plug in the values given:

\(\displaystyle =10,000\cdot \bigg(1+\frac{.08}{4}\bigg)^{(1)(4)}\)

\(\displaystyle =10,000 \cdot (1.02)^{4}\)

\(\displaystyle =10,824.32\)

Therefore, Jack makes $824.32 off his high-yield savings account. Now let's calculate the other interest:

\(\displaystyle \text{Interest}=\text{Principal} \cdot \text{ Interest Rate} \cdot \text{ Time}\)

\(\displaystyle =5,000 \cdot (0.06)\cdot (1)\)

\(\displaystyle =300\)

Add the two together, and we see that Jack makes a total of, \(\displaystyle \$1124.32\) off of his investments.

The formula to use for compounded interest is  

\(\displaystyle A=P\left(1+\frac{r}{n} \right )^{nt}\)

where P is the principal (original) amount, r is the interest rate (expressed in decimal form), n is the number of times per year the interest compounds, and t is the total number of years the money is left in the bank. In this problem, P=1,500, r=0.042, n=12, and t=3.

By plugging in, we find that Michelle will have about $1,701 at the end of three years.