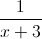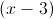We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Factoring Rational Expressions

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Factoring Rational Expressions

Simplify:

$\frac{x+3}{x^{2}+6x+9}$

Possible Answers:

$\left ( x+3 \right )^{2}$

$\left ( x+3 \right )$

$\frac{1}{\left ( x+3 \right )^{2}}$

$\frac{1}{x+3}$

$\left ( x-3 \right )$

Correct answer:

$\frac{1}{x+3}$

Explanation:

If we factors the denominator we get

$\left ( x+3 \right )^{2}$

Hence the rational expression becomes equal to

$\frac{\left ( x+3 \right )}{\left ( x+3 \right )^{2}}$

which is equal to $\frac{1}{\left ( x+3 \right )}$

Report an Error

Example Question #2 : Factoring Rational Expressions

Simplify.

$\frac{2x^2-4x-6}{4x-12}$

Possible Answers:

2x+2

$\frac{x+1}{2}$

x+1

The expression cannot be simplified.

$\frac{x^2-2x-3}{2(x-3)}$

Correct answer:

$\frac{x+1}{2}$

Explanation:

a. Simplify the numerator and denominator separately by pulling out common factors.

$\frac{2(x^2-2x-3)}{4(x-3)}$

b. Reduce if possible.

$\frac{x^2-2x-3}{2(x-3)}$

c. Factor the trinomial in the numerator.

$\frac{(x-3)(x+1)}{2(x-3)}$

d. Cancel common factors between the numerator and the denominator.

$\frac{{\color{Red} (x-3)}(x+1)}{2{\color{Red} (x-3)}}=\frac{x+1}{2}$

Report an Error

Example Question #1 : Factoring Rational Expressions

Transform the following equation from standard into vertex form:

y=3x^2+18x+15

Possible Answers:

y=3(x+3)^2+15

y=(3x+8)^2

y=3(x+3)^2-12

y=(3x+3)^2-18

y=(9x+2)^2-12

Correct answer:

y=3(x+3)^2-12

Explanation:

To take this standard form equation and transform it into vertex form, we need to complete the square. That can be done as follows:

$\small y=3x^2+18x+15$

y-15=3(x^2+6x)

We will complete the square on 3(x^2+6x) . In this case, our in our soon-to-be ax^2+bx+c is . We therefore want our $c=(\frac{1}{2}b)^2$ , so $\small c=(\frac{1}{2}(6))^2=9$ .

Since we are adding $\small 3\times9$ on the right side (as we are completing the square inside the parentheses), we need to add $\small 27$ on the left side as well. Our equation therefore becomes:

$\small y-15+27=3(x^2+6x+9)$

$\small y+12=3(x+3)^2$

Our final answer is therefore $\small y=3(x+3)^2-12$

Report an Error

Example Question #3 : Factoring Rational Expressions

Evaluate the following expression: $\small \small \frac{2x^2y^8}{5z^4}*\frac{10x^5z^5}{4y^6}$

Possible Answers:

$\small x^7y^2z$

$\small \frac{1}{\small x^7y^2z}$

$\small \frac{2y^1^4z^9}{5x^3}$

$\small \small \frac{5x^3}{2y^1^4z^9}$

$\small \frac{y^1^4z^9}{x^3}$

Correct answer:

$\small x^7y^2z$

Explanation:

When we multiply expressions with exponents, we need to keep in mind some rules:

Multiplied variables add exponents.

Divided variables subtract exponents.

Variables raised to a power multiply exponents.

Therefore, when we mulitiply the two fractions, we obtain:

$\small \frac{2x^2y^8}{5z^4}\ast\frac{10x^5z^5}{4y^6}=\frac{20x^7y^8z^5}{20y^6z^4}=x^7y^2z$

Our final answer is therefore $\small x^7y^2z$

Report an Error

Example Question #1 : Factoring Rational Expressions

Simplify:

$\frac{x^{2}+3x+2}{x+2}$

Possible Answers:

x+1

x-3

x-1

x+3

x+2

Correct answer:

x+1

Explanation:

First factor the numerator. We need two numbers with a sum of 3 and a product of 2. The numbers 1 and 2 satisfy these conditions:

(x+2)(x+1)

Now, look to see if there are any common factors that will cancel:

$\frac{(x+2)(x+1)}{x+2}$

The x+2 in the numerator and denominator cancel, leaving x+1 .

Report an Error

Example Question #5 : Factoring Rational Expressions

Simplify this rational expression: $\frac{x^2-14x+49}{x^2-2x-35}\cdot \frac{1}{x+5}$

Possible Answers:

$\frac{(x-7)^2}{x+5}$

$\frac{(x-7)^2}{(x+5)^2}$

$\frac{x-7}{(x+5)^2}$

$\frac{x-7}{x+5}$

None of the other answers.

Correct answer:

$\frac{x-7}{(x+5)^2}$

Explanation:

To see what can be simplified, factor the quadratic equations.

$\frac{(x-7)(x-7)}{(x-7)(x+5)}\cdot \frac{1}{x+5}$

Cancel out like terms:

$\frac{{\color{Red} (x-7)}(x-7)}{{\color{Red} (x-7)}(x+5)}\cdot \frac{1}{x+5}\rightarrow \frac{x-7}{x+5}\cdot \frac{1}{x+5}$

Combine terms:

$\frac{x-7}{(x+5)^2}$

Report an Error

Example Question #6 : Factoring Rational Expressions

Factor and simplify this rational expression: $\frac{(x+2)^2(x-3)(x+3)}{(x^2+2x+4)(x^2-6x+9)(x^2+6x+9)}$

Possible Answers:

$\frac{1}{(x+3)(x+3)}$

$\frac{1}{x^2+6x+9}$

$\frac{1}{(x-3)(x+3)}$

$\frac{1}{(x+3)}$

None of these.

Correct answer:

$\frac{1}{(x-3)(x+3)}$

Explanation:

$\frac{(x+2)^2(x-3)(x+3)}{(x^2+2x+4)(x^2-6x+9)(x^2+6x+9)}$

Completely factor all polynomials:

$\frac{(x+2)^2(x-3)(x+3)}{(x+2)(x+2)(x-3)(x-3)(x+3)(x+3)}$

Cancel like terms:

$\mathbf{\frac{1}{(x-3)(x+3)}}$

Report an Error

Example Question #7 : Factoring Rational Expressions

Factor $f(x)=\frac{x^2 + x - 12}{x^2 - x - 6}$ .

Possible Answers:

(x+4)(x+2)

$\frac{(x-3)}{(x+3)(x+2)}$

x(x+4)

$\frac{(x+4)}{(x+2)}$

$\frac{(x+3)(x+4)}{(x-3)(x+2)}$

Correct answer:

$\frac{(x+4)}{(x+2)}$

Explanation:

In the beginning, we can treat this as two separate problems, and factor the numerator and the denominator independently:

x^2 + x - 12 = (x+4)(x-3)

x^2 - x - 6 = (x+2)(x-3)

After we've factored them, we can put the factored equations back into the original problem:

$f(x)= \frac{(x+4)(x-3)}{(x+2)(x-3)}$

From here, we can cancel the (x-3) from the top and the bottom, leaving:

$f(x)=\frac{(x+4)}{(x+2)}$

Report an Error

Example Question #8 : Factoring Rational Expressions

Factor: $\frac{2x^2+8x-10}{16x-16}$

Possible Answers:

$\frac{x+5}{16}$

$\frac{x+3}{16}$

$\frac{x^2-4x-5}{8}$

$\frac{x^2-4x-5}{8x}$

$\frac{x+5}{8}$

Correct answer:

$\frac{x+5}{8}$

Explanation:

Factor a two out in the numerator.

2x^2+8x-10 = 2(x^2+4x-5)

Factor the trinomial.

2(x^2+4x-5) = 2(x-1)(x+5)

Factor the denominator.

16x-16 = 16(x-1)

Divide the terms.

$\frac{2(x-1)(x+5)}{16(x-1)}$

The answer is: $\frac{x+5}{8}$

Report an Error

Example Question #9 : Factoring Rational Expressions

Simplify to simplest terms.

$\frac{x^2-x-56}{x^2-15x+56}$

Possible Answers:

$\frac{x+7}{x-7}$

Correct answer:

Explanation:

The correct answer is . The numerator and denominator can both be factored to simpler terms:

$\frac{(x-8)(x+7)}{(x-8)(x-7)}$

The (x-8 ) terms will cancel out. Leaving $\frac{x+7}{x-7}$ . While this is an answer choice, it can be simplified further. Factoring out a from the denominator will allow the x-7 terms to cancel out leaving .

Report an Error

View Algebra 2 Tutors

Mohammed
Certified Tutor

University of Maryland-College Park, Bachelor of Science, Electrical Engineering. University of Maryland-College Park, Master...

View Algebra 2 Tutors

Steven
Certified Tutor

Florida International University, Bachelor of Science, Biology, General.

View Algebra 2 Tutors

Naman Sanjaykumar
Certified Tutor

LDRP Institute of Technology and Research, Bachelor, Mechanical Engineering. University of Windsor, Master's/Graduate, Mechan...

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Philadelphia, SSAT Tutors in San Diego, GMAT Tutors in San Diego, Algebra Tutors in Phoenix, GRE Tutors in Boston, English Tutors in Dallas Fort Worth, Reading Tutors in Philadelphia, French Tutors in New York City, SAT Tutors in Chicago, Statistics Tutors in Denver

Popular Courses & Classes

GMAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Atlanta, ACT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Phoenix, SSAT Courses & Classes in Seattle, ISEE Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Seattle, LSAT Courses & Classes in San Diego, SAT Courses & Classes in Seattle, LSAT Courses & Classes in Boston

Popular Test Prep

GRE Test Prep in Phoenix, MCAT Test Prep in Los Angeles, GRE Test Prep in Seattle, ISEE Test Prep in Denver, SAT Test Prep in Denver, MCAT Test Prep in Boston, GMAT Test Prep in Los Angeles, LSAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Philadelphia, GMAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Factoring Rational Expressions

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #1 : Factoring Rational Expressions

Example Question #2 : Factoring Rational Expressions

Example Question #1 : Factoring Rational Expressions

Example Question #3 : Factoring Rational Expressions

Example Question #1 : Factoring Rational Expressions

Example Question #5 : Factoring Rational Expressions

Example Question #6 : Factoring Rational Expressions

Example Question #7 : Factoring Rational Expressions

Example Question #8 : Factoring Rational Expressions

Example Question #9 : Factoring Rational Expressions

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: