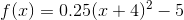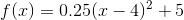We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Transformations

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Transformations

$f(x)=x^{2}$

$g(x)=4x^{2}-3$

How is the graph of g(x) different from the graph of f(x) ?

Possible Answers:

g(x) is wider than f(x) and is shifted to the right 3 units

g(x) is narrower than f(x) and is shifted down 3 units

g(x) is narrower than f(x) and is shifted to the left 3 units

g(x) is narrower than f(x) and is shifted up 3 units

g(x) is wider than f(x) and is shifted down 3 units

Correct answer:

g(x) is narrower than f(x) and is shifted down 3 units

Explanation:

Almost all transformed functions can be written like this:

g(x)=a[f(b(x-c))]+d

where f(x) is the parent function. In this case, our parent function is $f(x)=x^{2}$ , so we can write g(x) this way:

$g(x)=a[b(x-c)]^{2}+d$

Luckily, for this problem, we only have to worry about and .

represents the vertical stretch factor of the graph.

If is less than 1, the graph has been vertically compressed by a factor of . It's almost as if someone squished the graph while their hands were on the top and bottom. This would make a parabola, for example, look wider.
If is greater than 1, the graph has been vertically stretched by a factor of . It's almost as if someone pulled on the graph while their hands were grasping the top and bottom. This would make a parabola, for example, look narrower.

represents the vertical translation of the graph.

If is positive, the graph has been shifted up units.
If is negative, the graph has been shifted down units.

For this problem, is 4 and is -3, causing vertical stretch by a factor of 4 and a vertical translation down 3 units.

Report an Error

Example Question #2 : Transformations

Which of the following transformations represents a parabola shifted to the right by 4 and halved in width?

Possible Answers:

f(x)=2x^2+4

f(x) = 0.5(x-4)^2

f(x) = 2x^2 - 4

f(x) = 2(x-4)^2

f(x) = 2(x+4)^2

Correct answer:

f(x) = 2(x-4)^2

Explanation:

Begin with the standard equation for a parabola: f(x)=x^2 .

Horizontal shifts are represented by additions (leftward shifts) or subtractions (rightward shifts) within the parenthesis of the term. To shift 4 units to the right, subtract 4 within the parenthesis.

f(x)=(x-4)^2

The width of the parabola is determined by the magnitude of the coefficient in front of . To make a parabola narrower, use a whole number coefficient. Halving the width indicates a coefficient of two.

f(x) = 2(x-4)^2

Report an Error

Example Question #3 : Transformations

Which of the following represents a standard parabola shifted up by 2 units?

Possible Answers:

f(x)=x^2 + 2

f(x)=(x+2)^2

f(x)=(x-2)^2 - 4

f(x)=(x-2)^2 + 2

f(x)=(x-2)^2

Correct answer:

f(x)=x^2 + 2

Explanation:

Begin with the standard equation for a parabola: f(x)=x^2 .

Vertical shifts to this standard equation are represented by additions (upward shifts) or subtractions (downward shifts) added to the end of the equation. To shift upward 2 units, add 2.

f(x)=x^2+2

Report an Error

Example Question #4 : Transformations

Which of the following transformation flips a parabola vertically, doubles its width, and shifts it up by 3?

Possible Answers:

f(x)=-2x^2 +3

f(x)=-2(x^2 +3)

f(x)=-0.5x^2 +3

f(x)=-0.5x^2 +1.5

f(x)=-(0.5x^2 +3)

Correct answer:

f(x)=-0.5x^2 +3

Explanation:

Begin with the standard equation for a parabola: f(x)=x^2 .

Inverting, or flipping, a parabola refers to the sign in front of the coefficient of the . If the coefficient is negative, then the parabola opens downward.

f(x)=-x^2

The width of the parabola is determined by the magnitude of the coefficient in front of . To make a parabola wider, use a fractional coefficient. Doubling the width indicates a coefficient of one-half.

$f(x)=-(\frac{1}{2})x^2=-0.5x^2$

Vertical shifts are represented by additions (upward shifts) or subtractions (downward shifts) added to the end of the equation. To shift upward 3 units, add 3.

f(x)=-0.5x^2 +3

Report an Error

Example Question #5 : Transformations

Which of the following shifts a parabola six units to the right and five downward?

Possible Answers:

$f(x)=(x-\sqrt{6})^2-5$

$f(x)=(x-\sqrt{5})^2+6$

f(x)=(x+6)^2-5

f(x)=(x-5)^2-6

f(x)=(x-6)^2-5

Correct answer:

f(x)=(x-6)^2-5

Explanation:

Begin with the standard equation for a parabola: f(x)=x^2 .

Vertical shifts to this standard equation are represented by additions (upward shifts) or subtractions (downward shifts) added to the end of the equation. To shift downward 5 units, subtract 5.

f(x)=x^2-5

Horizontal shifts are represented by additions (leftward shifts) or subtractions (rightward shifts) within the parenthesis of the term. To shift 6 units to the right, subtract 6 within the parenthesis.

f(x)=(x-6)^2 - 5

Report an Error

Example Question #6 : Transformations

Which of the following transformations represents a parabola that has been flipped vertically, shifted to the right 12, and shifted downward 4?

Possible Answers:

f(x)=-(x-12)^2-4

f(x)=-[(x+12)^2+4]

f(x)=-(x+12)^2+4

f(x)=-[(x+12)^2-4]

f(x)=-(x+12)^2-4

Correct answer:

f(x)=-(x-12)^2-4

Explanation:

Begin with the standard equation for a parabola: f(x)=x^2 .

Horizontal shifts are represented by additions (leftward shifts) or subtractions (rightward shifts) within the parenthesis of the term. To shift 12 units to the right, subtract 12 within the parenthesis.

f(x) = (x-12)^2

Inverting, or flipping, a parabola refers to the sign in front of the coefficient of the . If the coefficient is negative, then the parabola opens downward.

f(x) = -(x-12)^2

Vertical shifts are represented by additions (upward shifts) or subtractions (downward shifts) added to the end of the equation. To shift downward 4 units, subtract 4.

f(x) = -(x-12)^2 - 4

Report an Error

Example Question #7 : Transformations

Which of the following transformations represents a parabola that has been shifted 4 units to the left, 5 units down, and quadrupled in width?

Possible Answers:

f(x) = 4(x-4)^2-5

f(x) = 0.25(x+4)^2-5

f(x) = 4(x+4)^2-5

f(x) = 0.25(x-4)^2-5

f(x) = 0.25(x-4)^2+5

Correct answer:

f(x) = 0.25(x+4)^2-5

Explanation:

Begin with the standard equation for a parabola: f(x)=x^2 .

Horizontal shifts are represented by additions (leftward shifts) or subtractions (rightward shifts) within the parenthesis of the term. To shift 4 units to the left, add 4 within the parenthesis.

f(x) = (x+4)^2

Vertical shifts are represented by additions (upward shifts) or subtractions (downward shifts) added to the end of the equation. To shift downward 5 units, subtract 5.

f(x) = 0.25(x+4)^2 - 5

Report an Error

Example Question #1 : Transformations

If the function y=1-x is shifted left 2 units, and up 3 units, what is the new equation?

Possible Answers:

y=x-2

y=-1-x

y=3-x

y=4-x

y=2-x

Correct answer:

y=2-x

Explanation:

Shifting y=1-x left 2 units will change the y-intercept from (0,1) to (0.-1) .

The new equation after shifting left 2 units is:

y=1-(x+2)=-1-x

Shifting up 3 units will add 3 to the y-intercept of the new equation.

The answer is: y=2-x

Report an Error

Example Question #1 : Transformations

If f(x)=x^2 , what is -f(x) ?

Possible Answers:

It is the same as f(x) .

It is the x^2 parabola reflected across the x-axis.

It is the x^2 parabola shifted to the right by 1.

It is the $x^{-2}$ function.

It is the x^2 parabola reflected across the y-axis.

Correct answer:

It is the x^2 parabola reflected across the x-axis.

Explanation:

It helps to evaluate the expression algebraically.

-f(x)=-x^2 . Any time you multiply a function by a -1, you reflect it over the x axis. It helps to graph for verification.

This is the graph of x^2

X 2

and this is the graph of -x^2

x 2

Report an Error

Example Question #10 : Transformations

If f(x)=e^x , what is f(-x) ?

Possible Answers:

It is the e^x graph shifted 1 to the right.

It is the e^x graph reflected across the y-axis.

It is the e^x graph reflected across the x-axis.

It is the e^x graph rotated about the origin.

It is the -e^x graph.

Correct answer:

It is the e^x graph reflected across the y-axis.

Explanation:

Algebraically, $f(-x)=e^{-x}$ .

This is a reflection across the y axis.

This is the graph of e^x

E x

And this is the graph of $e^{-x}$

E x

Report an Error

View Algebra 2 Tutors

Rodolfo
Certified Tutor

The University of Texas at San Antonio, Bachelor of Science, Mathematics.

View Algebra 2 Tutors

Barry
Certified Tutor

CUNY Lehman College, Bachelors, Math. CUNY Lehman College, Masters, Math Education.

View Algebra 2 Tutors

Michael
Certified Tutor

Furman University, Bachelor in Arts, History. Covenant Theological Seminary, Master of Divinity, Theology.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in Atlanta, SSAT Tutors in San Francisco-Bay Area, Biology Tutors in Boston, Chemistry Tutors in Chicago, GMAT Tutors in Denver, SAT Tutors in Chicago, English Tutors in Los Angeles, Calculus Tutors in San Diego, Reading Tutors in Washington DC, GRE Tutors in San Diego

Popular Courses & Classes

Spanish Courses & Classes in San Diego, SSAT Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in San Diego, MCAT Courses & Classes in Washington DC, ACT Courses & Classes in Phoenix, SSAT Courses & Classes in New York City, Spanish Courses & Classes in Los Angeles, Spanish Courses & Classes in Phoenix, ISEE Courses & Classes in Philadelphia, ACT Courses & Classes in Boston

Popular Test Prep

SAT Test Prep in Seattle, GMAT Test Prep in Seattle, ACT Test Prep in Phoenix, GMAT Test Prep in Atlanta, SSAT Test Prep in Phoenix, ISEE Test Prep in Boston, GRE Test Prep in San Francisco-Bay Area, SSAT Test Prep in Washington DC, ISEE Test Prep in Philadelphia, ISEE Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Transformations

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #1 : Transformations

Example Question #2 : Transformations

Example Question #3 : Transformations

Example Question #4 : Transformations

Example Question #5 : Transformations

Example Question #6 : Transformations

Example Question #7 : Transformations

Example Question #1 : Transformations

Example Question #1 : Transformations

Example Question #10 : Transformations

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: