All AP Calculus AB Resources
Example Questions
Example Question #47 : Integrals
If f(1) = 12, f' is continuous, and the integral from 1 to 4 of f'(x)dx = 16, what is the value of f(4)?
4
27
16
28
12
28
You are provided f(1) and are told to find the value of f(4). By the FTC, the following follows:
(integral from 1 to 4 of f'(x)dx) + f(1) = f(4)
16 + 12 = 28
Example Question #41 : Integrals
Find the limit.
lim as n approaches infiniti of ((4n3) – 6n)/((n3) – 2n2 + 6)
4
–6
0
1
nonexistent
4
lim as n approaches infiniti of ((4n3) – 6n)/((n3) – 2n2 + 6)
Use L'Hopitals rule to find the limit.
lim as n approaches infiniti of ((4n3) – 6n)/((n3) – 2n2 + 6)
lim as n approaches infiniti of ((12n2) – 6)/((3n2) – 4n + 6)
lim as n approaches infiniti of 24n/(6n – 4)
lim as n approaches infiniti of 24/6
The limit approaches 4.
Example Question #1 : Interpretations And Properties Of Definite Integrals
If a particle's movement is represented by 
The answer is 
now set 

Example Question #2 : Interpretations And Properties Of Definite Integrals
A particle's movement is represented by
At what time is the velocity at it's greatest?
The answer is at 6 seconds.

We can see that this equation will look like a upside down parabola so we know there will be only one maximum.
Now we set 

Example Question #3 : Interpretations And Properties Of Definite Integrals
What is the domain of 

Example Question #5 : Definite Integral Of The Rate Of Change Of A Quantity Over An Interval Interpreted As The Change Of The Quantity Over The Interval
If 
then at 

The answer is 8.
Example Question #4 : Interpretations And Properties Of Definite Integrals
What is the average value of the function 


The average function value is given by the following formula:
![Ave = \frac{1}{4} [x^{3}-\frac{5}{2}x^{2} + 7x]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/104059/gif.latex)


Example Question #5 : Interpretations And Properties Of Definite Integrals
If
then find 
We see the answer is 0 after we do the quotient rule.
Example Question #2 : Definite Integral Of The Rate Of Change Of A Quantity Over An Interval Interpreted As The Change Of The Quantity Over The Interval
Example Question #11 : Interpretations And Properties Of Definite Integrals
All AP Calculus AB Resources













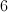



![(-\infty,-3]\cup [3,+\infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/27317/gif.latex)
























![Ave = \frac{1}{4}[(125-\frac{125}{2} + 35) - (1-\frac{5}{2}+7)] = 23](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/132675/gif.latex)















![\begin{align*}&\text{If the velocity function of a particle is known, finding the}\\&\text{distance it travels over a given interval of time is only a}\\&\text{matter of integrating the velocity function over this same interval.}\\&\text{Considering the function given:}\\&\text{Utilizing integral rules:}\\&\int[sin(ax)]=-\frac{cos(ax)}{a}\\&\int_{4}^{5.5}(\frac{(26sin(t + 2))}{3})dt=-\frac{(26cos(t + 2))}{3}|_{4}^{5.5}\\&\text{Now we just subtract the function value at the lower bound from that of the upper bound:}\\&\int_{4}^{5.5}(\frac{(26sin(t + 2))}{3})dt=-\frac{(26cos((5.5) + 2))}{3}-(-\frac{(26cos((4) + 2))}{3})\\&\int_{4}^{5.5}(\frac{(26sin(t + 2))}{3})dt=5.32\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/952944/gif.latex)









