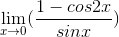All AP Calculus AB Resources
Example Questions
Example Question #1 : Derivative Interpreted As An Instantaneous Rate Of Change
Evaluate the following limit:
When 



Example Question #1 : Derivative Interpreted As An Instantaneous Rate Of Change
Find the instantaneous rate of change for the function,
at the point 
Find the instantaneous rate of change for the function,
at the point 
1) First compute the derivative of the function, since this will give us the instantaneous rate of change of the function as a function of 
2) Now evaluate the derivative at the value 
Therefore, 


Example Question #1 : Derivative Interpreted As An Instantaneous Rate Of Change
A particle is traveling in a straight line along the x-axis with position function 

To find the instantaneous rate of change of the particle at time 



And

Hence the instantaneous rate of change in position (or just 'velocity') of the particle at 

Example Question #2 : Derivative Interpreted As An Instantaneous Rate Of Change
Find the function values and as well as the instantaneous rate of change for the function 
Find the instantaneous rate of change for the function 
Evaluate the function at each value of
The instantaneous rate of change at any point 
Apply the product rule:
Therefore,
Now evaluate the derivative for each given value of 
Therefore, the instantaneous rate of change of the function 

Example Question #2 : Derivative Interpreted As An Instantaneous Rate Of Change
Given that v(t) is the velocity of a particle, find the particle's acceleration when t=3.
Not enough information provided
Given that v(t) is the velocity of a particle, find the particle's acceleration when t=3.
We are given velocity and asked to find acceleration. Our first step should be to find the derivative.
We can use our standard power rule for our 1st and 3rd terms, but we need to remember something else for our second term. Namely, that the derivative of 
With that in mind, let;s find v'(t)
Now, for the final push, we need to find the acceleration when t=3. We do this by plugging in 3 for t and simplifying.
So, our answer is 123.5
Example Question #4 : Derivative Interpreted As An Instantaneous Rate Of Change
Example Question #5 : Derivative Interpreted As An Instantaneous Rate Of Change
Example Question #6 : Derivative Interpreted As An Instantaneous Rate Of Change
Example Question #2 : Derivative Interpreted As An Instantaneous Rate Of Change
Example Question #8 : Derivative Interpreted As An Instantaneous Rate Of Change
All AP Calculus AB Resources