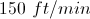All AP Calculus AB Resources
Example Questions
Example Question #1 : Integrals
Evaluate 
Does not exist
Even though an antideritvative of 







Example Question #2 : Integrals
The graph of a function 










The function 



Do not be confused by the use of 










If the function 


has for its' derivative 
Example Question #3 : Integrals
Evaluate
Here we could use the Fundamental Theorem of Calculus to evaluate the definite integral; however, that might be difficult and messy.
Instead, we make a clever observation of the graph of
Namely, that
This means that the values of the graph when comparing x and -x are equal but opposite. Then we can conclude that
Example Question #1 : Techniques Of Antidifferentiation
A projectile is shot up from a platform 




Separate velocity variables and solve.
Plug in intial conditions
Example Question #1 : Integrals
A gun sends a bullet straight up with a launch velocity of 220 ft/s. It reaches a height of 

The bullet will be at a height of 500 ft on the way up and on the way down.
We use the position equation 


We then plug that into the velocity equation, which is the derivative of the position function. 
We can see that plugging in the value of 



Example Question #1 : Techniques Of Antidifferentiation
The position of a particle as a function of time is given below:
At what values of 
In order to find the point at which the particle changes direction, we must determine whenever the velocity of the particle changes sign (from positive to negative, or from negative to positive).
We will need to have the function of the particle's velocity before we can determine where the velocity changes sign. Because the velocity is the derivative of position with respect to time, we can write the function for velocity, 
If we set 
The possible points where 

First, we can try a value less than 2, such as 1, and then a value between 2 and 4, such as 3. We will evaluate 


Thus, 

Lastly, we will evaluate the velocity at a value of 
The sign of the velocity has switched back to positive, so the particle does indeed change direction at 
The answer is 

Example Question #2 : Techniques Of Antidifferentiation
The speed of a car traveling on the highway is given by the following function of time:
Note that
What does this mean?
The car is not decelerating at time 
The car is not moving at time 
The car takes 
The car is not accelerating at time 
The car's speed is constantly changing at time 
The car is not moving at time 
The function 






Example Question #1 : Techniques Of Antidifferentiation
A jogger leaves City 
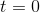
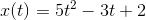
where 
Find the velocity of the jogger at 15 minutes.
To find velocity, one has to use the first derivative of 


Note the units have to be ft/min.
Example Question #2 : Integrals
Write the equation of a tangent line to the given function at the point.
y = ln(x2) at (e, 3)
y = (2/e)(x – e)
y – 3 = (x – e)
y – 3 = (2/e)(x – e)
y – 3 = ln(e2)(x – e)
y = (2/e)
y – 3 = (2/e)(x – e)
To solve this, first find the derivative of the function (otherwise known as the slope).
y = ln(x2)
y' = (2x/(x2))
Then, to find the slope in respect to the given points (e, 3), plug in e.
y' = (2e)/(e2)
Simplify.
y'=(2/e)
The question asks to find the tangent line to the function at (e, 3), so use the point-slope formula and the points (e, 3).
y – 3 = (2/e)(x – e)
Example Question #1 : Integrals
Find the equation of the tangent line at 
The answer is



All AP Calculus AB Resources


































![v(t)=x'(t)=\frac{d}{dx}[\frac{t^{3}}{3}-3t^{2}+8t]=\frac{3t^{2}}{3}-6t+8=t^{2}-6t+8](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/24744/gif.latex)