All AP Physics 1 Resources
Example Questions
Example Question #1 : Forces
A block of iron with mass 10kg is sitting on an incline that has an angle of 30 degrees above horizontal. What is the normal force on the block of iron?
The free body diagram of the system is shown below:


Since 

If you're confused as why it's cosine and not sine, think about the system practically. The flatter the slope is, the greater the normal force. The smaller an angle becomes (creating a flatter slope), the greater the value of cosine becomes, and subsequently the greater the normal force becomes.
Now we can simply plug in our given values:
Example Question #1 : Forces
A person tries to lift a very heavy 

First, calculate the gravitational force acting on the rock.
The exerts a force of 



Example Question #2 : Forces
Consider the following system:
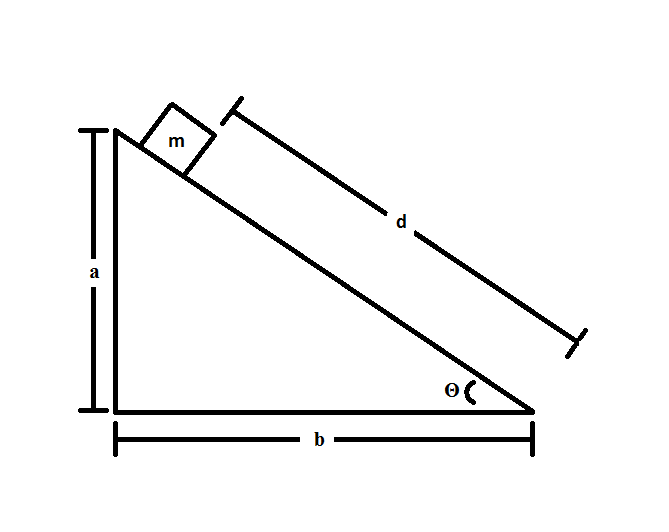
If the block is accelerating down the slope at an angle of 

There are two forces in play for this scenario: the first is gravity and the second is friction. We can use Newton's second law to solve this problem:
Substituing in the two forces we just mentioned:
Note that the force of friction is subtracted because it is in the opposite direction of the force of gravity. Now, substituting in expressions for our two forces, we get:
If you are unsure of whether to use cosine or sine for each force, think about the situation practically. The flatter the slope gets, the less the force of gravity will have an effect on moving the block down the plane, hence the use of the sine function. Also, the flatter the slope gets, the greater the normal force will become, hence the use of the cosine function.
Canceling out mass from the equation and rearranging to solve for the coefficient of friction, we get:
Example Question #2 : Forces
Consider the following system:

If the block travels down the slope at a constant speed and the coefficient of kinetic friction is 
There are two forces in play in this scenario. The first is gravity and the second is friction. Both depend on the angle of the slope. Since the block is traveling at a constant rate, we know the the gravitational and frictional force in the direction of the slope cancel each other out, and the net force is zero (there is no acceleration). Therefore, we can write:
Substituting in expressions for each force, we get:
If you are unsure of whether to use cosine or sine for each force, think about the situation practically. The flatter the slope gets, the less the force of gravity will have an effect on moving the block down the plane, hence the use of the sine function. Also, the flatter the slope gets, the greater the normal force will become, hence the use of the cosine function.
Canceling out mass and solving for the angle on one side of the equation, we get:
This is an important property to know! When an object travels down a slope at a constant rate, the tangent of the angle of the slope is equal to the coefficient of kinetic friction.
Example Question #1 : Normal Force And Weight
Consider the following system:

If 
There are two forces at play in this scenario: the force of friction and the force of gravity. If the block is stationary, that means that the two forces cancel each other out. Therefore, we can write:
Substituting in expressions for each force, we get:
If you are unsure of whether to use cosine or sine for each force, think about the situation practically. The flatter the slope gets, the less the force of gravity will have an effect on trying to move the block down the plane, hence the use of the sine function. Also, the flatter the slope gets, the greater the normal force will become, hence the use of the cosine function.
Example Question #1 : Normal Force And Weight
Consider the following system:

Side 



There are two forces in play in this scenario: gravity and friction. We can use Newton's second law to form an expression with these forces:
Substituting in expressions for each force, we get:
If you are unsure of whether to use cosine or sine for each force, think about the situation practically. The flatter the slope gets, the less the force of gravity will have an effect on moving the block down the plane, hence the use of the sine function. Also, the flatter the slope gets, the greater the normal force will become, hence the use of the cosine function.
Canceling out mass and rearranging for the coefficient of friction, we get:
Example Question #2 : Normal Force And Weight
Consider the following system:
If the normal force on the block is 

We need to develop an expression for the normal force on the block to solve this problem:
If you are unsure of whether to use sine or cosine, think about the system practically: the flatter the system gets, the larger the normal force will become; hence the use of the cosine function.
Rearranging for mass, we get:
Example Question #8 : Normal Force And Weight
What is the magnitude of the normal force exerted on an an object weighing 5kg, which is on a 

Cannot be determined without knowing the height of the object from the ground
Recall that the formula for determining the magnitude of the normal force on an incline is given by:
Here, 



In our case:
Example Question #1 : Specific Forces
An object with a mass of 10kg is resting on a horizontal table. What is the normal force acting on the object?

The normal force points perpendicular to the force of gravity (opposite direction) and is equal in magnitude. Because the force of gravity is equal to 
Example Question #1 : Normal Force And Weight
A person who weighs 

There is not enough information given to solve this problem
The person's weight will not change, it will remain at
In this question, we're presented with a scenario where a person weighing 
Let's begin our analysis by first considering the person to be at rest in the elevator. In this situation, it's useful to picture a free-body diagram of the person and all of the forces acting on him/her. While at rest, there is no net force acting on this individual. Since there is no net force in the y-direction, that means that the upward forces must be exactly balanced by the downward forces. The downward force acting on the individual is the force due to gravity, while the upward force is the normal force of the elevator's floor acting on the individual.
Put another way:
Next, let's derive an expression while considering the upward acceleration of the elevator. In such a situation, there is now a net force acting on the individual, and that net upward force is due to the elevator's acceleration. Just as it was while at rest, the downward force acting on the individual in this case is still the force due to gravity, and the upward force acting on the individual is the normal force of the elevator's floor.
Written in equation form, we have:
Notice that we are solving for the new value of the normal force while the elevator is accelerating. The reason why the normal force gives us the person's weight is due to Newton's third law. When the elevator accelerates upward, the elevator exerts a (normal) force on the individual that is equal in magnitude to the person's weight, but with reversed directionality.
Finally, we can calculate the person's mass:
Plugging the relavent values into the above expression that we've derived will give us our answer.
Notice that this value is greater than the 
Certified Tutor
Certified Tutor
All AP Physics 1 Resources



























































































