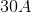First, find the total resistance of the circuit. Since the resistors are in parallel, use the following formula:

$\displaystyle \frac{1}{R1}+\frac{1}{R2}=\frac{1}{R_{total}}$

Plug in known values.

$\displaystyle \frac{1}{10\Omega}+\frac{1}{20\Omega}=\frac{1}{R_{total}}$ 

$\displaystyle R_{total}=6.66\Omega$

Next, use Ohm's law to find current.

$\displaystyle V=IR$

Plug in known values.

$\displaystyle I=\frac{25V}{6.66\Omega}=3.75A$

Use Ohm's law to find the current passing through each resistor. Because they are in series, they have the same amount of current. Once we get the current, we can plug in the resistance for each resistor to find its potential drop.

$\displaystyle I&=\frac{V_{tot}}{R_{tot}}$

$\displaystyle I=\frac{12V}{12\Omega}$

$\displaystyle I= 1A$

Now, find the potential drop across the $\displaystyle 4\Omega$ resistor.

$\displaystyle V&=IR$

$\displaystyle V=(1A)(4\Omega)$

$\displaystyle V= 4V$

Therefore, the potential drop across the $\displaystyle 4\Omega$ resistor is $\displaystyle 4V$

Even though there is no resistor, Ohm's law still applies. Use it to find the resistance of the wire.

$\displaystyle R&=\frac{V}{I}$

$\displaystyle R= \frac{4.5V}{0.90A}$

$\displaystyle R= 5\Omega$

The resistance of the copper wire is $\displaystyle 5\Omega$

First, find the total resistance of the circuit.

$\displaystyle R_1$ and $\displaystyle R_2$ are in parallel, so we find the equivalent resistance by using the following formula:

$\displaystyle \frac{1}{R_{1}}+\frac{1}R_{2}=\frac{1}{R_{1+2}}$ 

$\displaystyle \frac{1}{3}+\frac{1}{6}=\frac{1}{2}=\frac{1}{R_{1+2}}$

$\displaystyle R_{1+2}=2\Omega$

Next, add the series resistors together.

$\displaystyle R_{1+2}+R_3+R_4=R_{total}$

$\displaystyle R_{total}=8\Omega$

Use Ohm's law to find the current through the system. 

$\displaystyle V=IR$

$\displaystyle (V_1+V_2)=IR$

$\displaystyle 9V=I\cdot 8\Omega$

$\displaystyle I=\frac{9}{8}A$

Since $\displaystyle R_1$ and $\displaystyle R_2$ are in parallel, they will have the same voltage drop accross them. 

$\displaystyle V_{1+2}=\frac{9}{8}A \cdot R_{1+2}$

$\displaystyle V_{1+2}=\frac{9}{8}A\cdot 2\Omega$

$\displaystyle V_{1+2}=\frac{9}{4}V$

First, find the total resistance of the circuit.

$\displaystyle R_1$ and $\displaystyle R_2$ are in parallel, so we find their equivalent resistance by using the following formula:

$\displaystyle \frac{1}{R_{1}}+\frac{1}R_{2}=\frac{1}{R_{1+2}}$

$\displaystyle \frac{1}{3}+\frac{1}{6}=\frac{1}{R_{1+2}}$

$\displaystyle \frac{3}{6}=\frac{1}{R_{1+2}}}$

$\displaystyle R_{1+2}=2\Omega$

Next, add the series resistors together.

$\displaystyle R_{1+2}+R_3+R_4=R_{total}$

$\displaystyle R_{total}=8\Omega$

Use Ohm's law to find the current in the system.

$\displaystyle V=IR$

$\displaystyle (V_1+V_2)=IR$

$\displaystyle 9V=I\cdot 8\Omega$

$\displaystyle I=\frac{9}{8}A$

The current through $\displaystyle R_1$ and $\displaystyle R_2$ needs to add up to the total current, since they are in parallel.

$\displaystyle I_1 + I_2 =I_{total}$

$\displaystyle I_1 + I_2 =\frac{9}{8}A$

Also, the voltage drop across them need to be equal, since they are in parallel.

$\displaystyle V_1=V_2$

$\displaystyle I_1R_1=I_2R_2$

$\displaystyle I_1\cdot3\Omega=I_2\cdot 6\Omega$ 

Set up a system of equations.

$\displaystyle I_1\cdot3\Omega=I_2\cdot 6\Omega$

$\displaystyle I_1 + I_2 =\frac{9}{8}A$

Solve. 

$\displaystyle 2I_2=I_1$

$\displaystyle 3I_2=\frac{9}{8}A$

$\displaystyle I_2=\frac{3}{8}A$

First, find the total resistance of the circuit.

$\displaystyle R_1$ and $\displaystyle R_2$ are in parallel, so we find their equivalent resistance by using the following formula:

$\displaystyle \frac{1}{R_{1}}+\frac{1}R_{2}=\frac{1}{R_{1+2}}$

$\displaystyle \frac{1}{3}+\frac{1}{6}=\frac{1}{R_{1+2}}$

$\displaystyle \frac{3}{6}=\frac{1}{R_{1+2}}}$

$\displaystyle R_{1+2}=2\Omega$

Next, add the series resistors together.

$\displaystyle R_{1+2}+R_3+R_4=R_{total}$

$\displaystyle R_{total}=8\Omega$

Use Ohm's law to find the current in the system.

$\displaystyle V=IR$

$\displaystyle (V_1+V_2)=IR$

$\displaystyle 9V=I\cdot 8\Omega$

$\displaystyle I=\frac{9}{8}A$

In series, all resistors will have the same current.

Thus, the current through $\displaystyle R_3$ is the same as through the rest of the circuit.

First, find the total resistance of the circuit.

$\displaystyle R_1$ and $\displaystyle R_2$ are in parallel, so we find their equivalent resistance by using the following formula:

$\displaystyle \frac{1}{R_{1}}+\frac{1}R_{2}=\frac{1}{R_{1+2}}$

$\displaystyle \frac{1}{3}+\frac{1}{6}=\frac{1}{R_{1+2}}$

$\displaystyle \frac{3}{6}=\frac{1}{R_{1+2}}}$

$\displaystyle R_{1+2}=2\Omega$

Next, add the series resistors together.

$\displaystyle R_{1+2}+R_3+R_4=R_{total}$

$\displaystyle R_{total}=8\Omega$

Use Ohm's law to find the current in the system.

$\displaystyle V=IR$

$\displaystyle (V_1+V_2)=IR$

$\displaystyle 9V=I\cdot 8\Omega$

$\displaystyle I=\frac{9}{8}A$

$\displaystyle R_1$ and $\displaystyle R_2$ will have the same voltage drop across them, as they are in parallel, and are equivalent to the combined resistor $\displaystyle R_{1+2}$

$\displaystyle V=\frac{9}{8}A\cdot R_{3}$

$\displaystyle V=\frac{9}{8}A\cdot 3\Omega$

$\displaystyle V=\frac{27}{8}V$

First, find the total resistance of the circuit.

$\displaystyle R_1$ and $\displaystyle R_2$ are in parallel, so we find their equivalent resistance by using the following formula:

$\displaystyle \frac{1}{R_{1}}+\frac{1}R_{2}=\frac{1}{R_{1+2}}$

$\displaystyle \frac{1}{3}+\frac{1}{6}=\frac{1}{R_{1+2}}$

$\displaystyle \frac{3}{6}=\frac{1}{R_{1+2}}}$

$\displaystyle R_{1+2}=2\Omega$

Next, add the series resistors together.

$\displaystyle R_{1+2}+R_3+R_4=R_{total}$

$\displaystyle R_{total}=8\Omega$

Use Ohm's law to find the current in the system.

$\displaystyle V=IR$

$\displaystyle (V_1+V_2)=IR$

$\displaystyle 9V=I\cdot 8\Omega$

$\displaystyle I=\frac{9}{8}A$

$\displaystyle R_1$ and $\displaystyle R_2$ will have the same voltage drop across them, as they are in parallel, and are equivalent to the combined resistor $\displaystyle R_{1+2}$

$\displaystyle V=\frac{9}{8}A\cdot R_{1+2}$

$\displaystyle V=\frac{9}{8}A\cdot 2\Omega$

$\displaystyle V=\frac{9}{4}V$

$\displaystyle R_1$, $\displaystyle R_2$, and $\displaystyle R_3$ are in parallel, so we add them by using:

$\displaystyle \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} = \frac{1}{R_{1,2,3}}}$

We find that $\displaystyle R_{1,2,3} = \frac{15}{13}\Omega$

$\displaystyle R_{1,2,3}$, $\displaystyle R_4$, and $\displaystyle R_5$ are in series. So we use:

$\displaystyle R_{1,2,3}+R_4 +R_5 = R_{total}$

$\displaystyle \frac{15}{13}\Omega+1\Omega +1\Omega = R_{total}$

$\displaystyle R_{total}=\frac{67}{13}\Omega$

$\displaystyle R_1$, $\displaystyle R_2$, and $\displaystyle R_3$ are in parallel, so we add them by using:

$\displaystyle \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} = \frac{1}{R_{1,2,3}}}$

We find that $\displaystyle R_{1,2,3} = \frac{15}{13}\Omega$

$\displaystyle R_{1,2,3}$, $\displaystyle R_4$, and $\displaystyle R_5$ are in series. So we use:

$\displaystyle R_{1,2,3}+R_4 +R_5 = R_{total}$

$\displaystyle \frac{15}{13}\Omega+1\Omega +1\Omega = R_{total}$

$\displaystyle R_{total}=\frac{67}{13}\Omega$

First, we need to find the total current of the circuit, we simply use:

$\displaystyle V=IR$

$\displaystyle I=\frac{V}{R}$

$\displaystyle I=\frac{15V}{\frac{67}{13}\Omega}$

$\displaystyle I=\frac{195}{67} amps$

Because $\displaystyle R_1$, $\displaystyle R_2$ and $\displaystyle R_3$ are in parallel,

$\displaystyle I_1+I_2+I_3=I_{total}$

Also, the voltage drop must be the same across all three

$\displaystyle V_1=V_2=V_3$

Using

$\displaystyle V=IR$

$\displaystyle I_1R_1=I_2R_2=I_3R_3$

Using algebraic subsitution we get:

$\displaystyle I_3+I_3 \frac{R_3}{R_1}+I_3 \frac{R_3}{R_2}=I_{total}$

Solving for $\displaystyle I_3$

$\displaystyle \frac{I_{Total}}{1+\frac{R_3}{R_1}+\frac{R_3}{R_2}}=I_3$

$\displaystyle \frac{I_{Total}}{1+\frac{6}{2}+\frac{6}{5}}=I_3$

 $\displaystyle .560 amps=I_3$