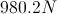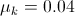When given a question about the angle of a ramp, compare it to the extreme angles: 0^o and 90^o.

1. When the ramp has an angle of 0^o, the net force 0. The force due to gravity must equal the normal force; thus the normal force is at a maximum value.

2. When the angle of the ramp is 90^o, the full force of gravity is experienced by the box, and there is no normal force. The net force is equal to the force of gravity. Remember that $\displaystyle F_g=mgsin\Theta$, so then theta is 90^o, force of gravity is at a maximum.

When we decrease the angle of the ramp, we get closer to scenario 1. As a result, we can conclude that the normal force on the box increases, rather than decreases.

The normal force of the woman is measured by the scale. While accelerating upward, the scale should read a larger weight than when it is at rest. When the elevator is moving upward at a constant speed, the scale should read the same as when it is at rest. This is because the normal force is generated to counter the downward forces pushing against the floor. When the elevator is accelerating, there is a net upward force from the acceleration as well as the normal force to counter gravity. The normal force generates an upward acceleration. When moving at a constant speed, there is no upward acceleration and the normal force acts only to counter gravity. The normal force, and scale reading, will thus be greater during the period of acceleration.

To find the normal force on the incline, we use the relationship:

$\displaystyle F_{N}=mg\cos(\theta )$

This provides the magnitude of the force of gravity in the direction perpendicular to the incline. Normal force will always act in the direction perpendicular to the surface, and in this case will be equal and opposite to the force of gravity. We then plug in the mass and gravitational acceleration to find the normal force on this block:

$\displaystyle F_N=(10kg)(9.8\frac{m}{s^2})\cos(30^o)$

$\displaystyle F_N=84.9N$

The normal force is generated as a result of a force against a solid surface. As per Newton's third law, the surface will exert an equal and opposite force on the object in contact. If an object is resting on a flat surface, then the normal force will be working to counter the weight of the object due to gravity.

The normal force acting on the bench with five players is equal and opposite to the total weight of the bench and players. Keep in mind that weight acts in the downward direction.

$\displaystyle F_N=-F_g$

$\displaystyle F_g=-(400N+4500N)=-4900N$

$\displaystyle F_N=4900N$

When the two players stand up, the new normal force is reduced.

$\displaystyle F_g=(-4900N)-(-1000N-1200N)=-2700N$

$\displaystyle F_N=2700N$

The difference in the normal force is:

$\displaystyle 4900N-2700N=2200N$

We could also have found this change by adding the weights of the two players who stood.

First, calculate the gravitational force acting on the rock.

$\displaystyle F_g=mg=(70\ \text{kg})(9.8\ \frac{\text{m}}{\text{s}^2})=686\ \text{N}$

The exerts a force of $\displaystyle 686N$ downward, meaning that if the person exerted at least $\displaystyle 686N$, then he or she would have been able to lift it up. Instead, the person applied only $\displaystyle 500N$. This means that the person needed to apply $\displaystyle 186N$ of additional force to lift the rock.

$\displaystyle 686N-500N=186N$

We know that normal force on a flat surface is equal and opposite the force of gravity.

$\displaystyle F_N=-mg$

$\displaystyle F_N=-(20kg)(-9.8\frac{m}{s^2})=196N$

Then, find the friction force between the crate and the floor using the equation:

$\displaystyle F_f=\mu F_N$

$\displaystyle F_{f}=(196N)(0.8)=156.8N$

This force is the minimum force required to start moving the crate.

The maximum force that can be applied will be equal to the maximum value of the static friction force. The formula for friction is:

$\displaystyle F_{friction}=\mu*F_{Normal}$

We also know that the normal force is equal and opposite the force of gravity.

$\displaystyle F_{Normal}=-(F_g)=-mg$

Substituting to the original equation, we can rewrite the force of friction.

$\displaystyle F_{Friction}=\mu*-(mg)$

Using the given values for the coefficient of friction and mass, we can calculate the force using the acceleration of gravity.

$\displaystyle F_{friction}=0.4*-(40 kg*-9.8\frac{m}{s^2})= 156.8 N$
 

Work is equal to the change in energy of the system. We are given the weight of the box and the vertical displacement, which will allow us to calculate the change in potential energy. This will be the total work required to move the box against gravity.

$\displaystyle W_g=\Delta PE=mg\Delta h$

$\displaystyle W_g=(50N)(4m)=200J$

The remaining work that the man exerts must have been used to counter the force of friction acting against his motion.

$\displaystyle W_{total}=W_g+W_f$

$\displaystyle W_f=270J-200J=70J$

Now we know the work performed by friction. Using this value, we can work to solve for the force of friction and the coefficient of friction. First, we will need to use a second formula for work:

$\displaystyle W=Fd$

In this case, the distance will be the distance traveled along the surface of the incline. We can solve for this distance using trigonometry.

$\displaystyle \sin(\theta)=\frac{opp}{hyp}$

$\displaystyle \sin(30^o)=\frac{4m}{d}=$

$\displaystyle d=\frac{4m}{\frac{1}{2}}=8m$

We know the work done by friction and the distance traveled along the incline, allowing us to solve for the force of friction.

$\displaystyle W_f=F_f*d$

$\displaystyle 70J=F_f(8m)$

$\displaystyle F_f=\frac{70J}{8m}=8.75N$

Finally, use the formula for frictional force to solve for the coefficient of friction. Keep in mind that the force on the box due to gravity will be equal to $\displaystyle mg\cos(\theta)$.

$\displaystyle F_f=\mu F_N=\mu(-F_g)$

$\displaystyle F_g=mg\cos(\theta)$

$\displaystyle F_f=\mu(-mg\cos(\theta))$

Plug in our final values and solve for the coefficient of friction.

$\displaystyle 8.75N=-\mu(-50N)\cos(30^o)=\mu(50N)(0.866)$

$\displaystyle \mu=\frac{8.75N}{50N(0.866)}=0.20$

In order for the crate to not slide, the truck has to exert a frictional force on it. The force of friction is related to the normal force by the coefficient of friction.

$\displaystyle F_N=mg$

$\displaystyle F_{friction}=\mu_sF_N=\mu_smg$

This frictional force comes from the acceleration of the truck, based on Newton's second law.

$\displaystyle F_T=ma_T$

The two forces will be equal when the truck is at maximum acceleration without the crate moving.

$\displaystyle F_T=F_f$

$\displaystyle ma=\mu_smg$

Solve for the acceleration.

$\displaystyle a=\mu_sg$

$\displaystyle a=(0.4)(9.8\frac{m}{s^2})$

$\displaystyle a=3.92\frac{m}{s^2}$

Since the box is moving when the net force on the box is determined, we can calculate the coefficient of kinetic friction for the box. The first step is determining what the net force on the box would be in the absence of friction. The net force on the box is given by the equation $\displaystyle \small F = mgsin\Theta$.

$\displaystyle \small F = (2kg)(10\frac{m}{s^{2}})sin(60^{\circ}) = 17.3N.$

The difference between the frictionless net force and the net force with friction is 0.8N. This means that the force of kinetic friction on the box is 0.8N, acting opposite the direction of motion. Knowing this, we can solve for the coefficient of kinetic friction using the equation $\displaystyle \small f_{k} = \mu_{k}F_{n}$

$\displaystyle \small 0.8 = (mgcos\Theta)(\mu _{k})$

$\displaystyle \small 0.8 = (2kg)(10cos(60^{\circ}))\mu_{k}$

$\displaystyle \small \mu_{k} = 0.08$