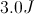We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

AP Physics C: Mechanics : Potential Energy

Study concepts, example questions & explanations for AP Physics C: Mechanics

Create An Account

All AP Physics C: Mechanics Resources

2 Diagnostic Tests 92 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Energy

Calculate how much potential energy a vertical standing spring gains if someone puts a 4kg box on top of it. Take the spring constant to be 120N/s.

Possible Answers:

8.0J $\displaystyle 8.0J$

3.0J $\displaystyle 3.0J$

8.9 J $\displaystyle 8.9 J$

12.2 J $\displaystyle 12.2 J$

6.5 J $\displaystyle 6.5 J$

Correct answer:

6.5 J $\displaystyle 6.5 J$

Explanation:

First, find out how much the spring compresses when the 4kg box is put on top of it. To find this, consider what forces are acting on the box when it is resting on the spring. The forces acting on it are the upward spring force, $\displaystyle F_s=-kx$, and the downward gravitational force,$\displaystyle F_g=mg$; thus, the net force acting on the box is given by the equation below.

$F_{net}=F_s-F_g=-kx-mg=0$ $\displaystyle F_{net}=F_s-F_g=-kx-mg=0$

We have chosen the upward direction to be positive and the downward direction to be negative. The net force is equal to zero because the box is at rest. Solve for x.

$x=-\frac{mg}{k}$ $\displaystyle x=-\frac{mg}{k}$

$x=-\frac{(4\ kg)(-9.8\ \frac{m}{s^2})}{120\ \frac{N}{m}}$ $\displaystyle x=-\frac{(4\ kg)(-9.8\ \frac{m}{s^2})}{120\ \frac{N}{m}}$

$x=0.33\ \text{m}$ $\displaystyle x=0.33\ \text{m}$

Then use this value to find the potential energy of the spring.

$U=\frac{1}{2}kx^2$ $\displaystyle U=\frac{1}{2}kx^2$

$U=\frac{1}{2}(120\ \frac{N}{m})(0.33\ m)^2$ $\displaystyle U=\frac{1}{2}(120\ \frac{N}{m})(0.33\ m)^2$

$U=6.5\ J$ $\displaystyle U=6.5\ J$

So when the box is placed on top of the spring, the spring gains a potential energy of 6.5J.

Report an Error

Example Question #11 : Energy

A man throws a 5kg ball straight up. At the top of its trajectory, the ball has a potential energy of 160 Joules. What is the highest point the ball reaches if it is thrown from the level of the ground?

$g=10\frac{m}{s^2}$ $\displaystyle g=10\frac{m}{s^2}$

Possible Answers:

10.5m $\displaystyle 10.5m$

4.8m $\displaystyle 4.8m$

3.2m $\displaystyle 3.2m$

6.4m $\displaystyle 6.4m$

14.4m $\displaystyle 14.4m$

Correct answer:

3.2m $\displaystyle 3.2m$

Explanation:

The equation for potential energy is:

PE=mgh $\displaystyle PE=mgh$

We can rearrange to solve for the height:

$h=\frac{PE}{mg}$ $\displaystyle h=\frac{PE}{mg}$

Plug in our given values to solve:

$h=\frac{160J}{(5kg)(10\frac{m}{s^2})}=3.2m$ $\displaystyle h=\frac{160J}{(5kg)(10\frac{m}{s^2})}=3.2m$

Report an Error

Example Question #12 : Energy

A man throws a 5kg ball straight up. At the top of its trajectory, the ball has a potential energy of 160 Joules. At what velocity does the man initially throw the ball?

Possible Answers:

$5\frac{m}{s}$ $\displaystyle 5\frac{m}{s}$

$16\frac{m}{s}$ $\displaystyle 16\frac{m}{s}$

$24\frac{m}{s}$ $\displaystyle 24\frac{m}{s}$

$10\frac{m}{s}$ $\displaystyle 10\frac{m}{s}$

$8\frac{m}{s}$ $\displaystyle 8\frac{m}{s}$

Correct answer:

$8\frac{m}{s}$ $\displaystyle 8\frac{m}{s}$

Explanation:

We can use conservation of energy to find the velocity required to launch the ball.

$KE= \frac{1}{2}mv^2$ $\displaystyle KE= \frac{1}{2}mv^2$

$PE = KE \rightarrow 160 = \frac{1}{2}mv^2$ $\displaystyle PE = KE \rightarrow 160 = \frac{1}{2}mv^2$

$\displaystyle 320 = (5)v^2$

$\displaystyle v^2 = 64$

$v = 8\ \frac{m}{s}$ $\displaystyle v = 8\ \frac{m}{s}$

Report an Error

Example Question #231 : Ap Physics C

$G \approx (20/3) *10^{-11} \ \frac{m^3}{kg*s^2}, \quad M_{earth} \approx 6*10^{24}\ kg, \quad R_{earth} \approx 6000 \ km$ $\displaystyle G \approx (20/3) *10^{-11} \ \frac{m^3}{kg*s^2}, \quad M_{earth} \approx 6*10^{24}\ kg, \quad R_{earth} \approx 6000 \ km$

A man launches a 5kg ball straight up from sea level. Disregarding drag, if the man would like to launch the ball into an escape trajectory from earth's gravity, approximately how fast must he launch the ball (in meters per second)?

$G=6.67*10^{-11}\frac{m^3}{s^2kg}$ $\displaystyle G=6.67*10^{-11}\frac{m^3}{s^2kg}$

$M_E=6*10^{24}kg$ $\displaystyle M_E=6*10^{24}kg$

$\displaystyle r_E=6*10^6m$

Possible Answers:

$21000\frac{m}{s}$ $\displaystyle 21000\frac{m}{s}$

$11000\frac{m}{s}$ $\displaystyle 11000\frac{m}{s}$

$5000\frac{m}{s}$ $\displaystyle 5000\frac{m}{s}$

$7000\frac{m}{s}$ $\displaystyle 7000\frac{m}{s}$

$44000\frac{m}{s}$ $\displaystyle 44000\frac{m}{s}$

Correct answer:

$11000\frac{m}{s}$ $\displaystyle 11000\frac{m}{s}$

Explanation:

In order to launch the ball at a velocity that escapes Earth's gravity, the kinetic energy must overcome the gravitational pull of the Earth. We can use conservation of energy to make the kinetic energy and gravitational potential energies equivalent.

$KE_{escape} = \frac{1}{2}m v_{escape}^2$ $\displaystyle KE_{escape} = \frac{1}{2}m v_{escape}^2$

$U_{gravitational} = \frac{GMm}{r}$ $\displaystyle U_{gravitational} = \frac{GMm}{r}$

$KE_{e} = U_{g}$ $\displaystyle KE_{e} = U_{g}$

$\frac{1}{2}mv_{e}^2= \frac{GMm}{r}$ $\displaystyle \frac{1}{2}mv_{e}^2= \frac{GMm}{r}$

Rearrange to solve for the escape velocity:

$v_e = \sqrt{\frac{2GM}{r}}$ $\displaystyle v_e = \sqrt{\frac{2GM}{r}}$

Finally, plug in our values and solve.

$v_e= \sqrt{\frac{2(6.67*10^{-11})(6*10^{24})}{6*10^6}}$ $\displaystyle v_e= \sqrt{\frac{2(6.67*10^{-11})(6*10^{24})}{6*10^6}}$

$v_e=\sqrt{\frac{72}{6}*10^{7}} =\sqrt{1.2*10^{8}} \approx\sqrt{121*10^{6}} = 11000\ \frac{m}{s}$ $\displaystyle v_e=\sqrt{\frac{72}{6}*10^{7}} =\sqrt{1.2*10^{8}} \approx\sqrt{121*10^{6}} = 11000\ \frac{m}{s}$

Report an Error

View Tutors

Nicole
Certified Tutor

College of Charleston, Bachelor of Philosophy, Philosophy.

View Tutors

Preetham
Certified Tutor

University of California-San Diego, Bachelor of Science, Structural Engineering.

View Tutors

Ann
Certified Tutor

Wright State University-Main Campus, Bachelor of Science, Mathematics and Computer Science. Western Governors University, Mas...

All AP Physics C: Mechanics Resources

2 Diagnostic Tests 92 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Phoenix, SAT Tutors in San Francisco-Bay Area, English Tutors in Boston, Biology Tutors in Washington DC, GMAT Tutors in New York City, SAT Tutors in New York City, Spanish Tutors in Seattle, ACT Tutors in Los Angeles, GMAT Tutors in San Diego, Chemistry Tutors in Seattle

Popular Courses & Classes

SSAT Courses & Classes in Atlanta, MCAT Courses & Classes in Houston, GMAT Courses & Classes in Houston, ACT Courses & Classes in Los Angeles, GRE Courses & Classes in Seattle, GRE Courses & Classes in Atlanta, ISEE Courses & Classes in Denver, SAT Courses & Classes in Miami, GMAT Courses & Classes in Miami, GRE Courses & Classes in Denver

Popular Test Prep

SSAT Test Prep in New York City, SAT Test Prep in New York City, GRE Test Prep in San Diego, GMAT Test Prep in Los Angeles, ISEE Test Prep in Dallas Fort Worth, SAT Test Prep in Boston, GMAT Test Prep in Chicago, GRE Test Prep in San Francisco-Bay Area, SAT Test Prep in Denver, SAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Physics C: Mechanics : Potential Energy

Study concepts, example questions & explanations for AP Physics C: Mechanics

All AP Physics C: Mechanics Resources

Example Questions

Example Question #2 : Energy

Example Question #11 : Energy

Example Question #12 : Energy

Example Question #231 : Ap Physics C

All AP Physics C: Mechanics Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: