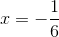All Calculus 1 Resources
Example Questions
Example Question #1 : Points
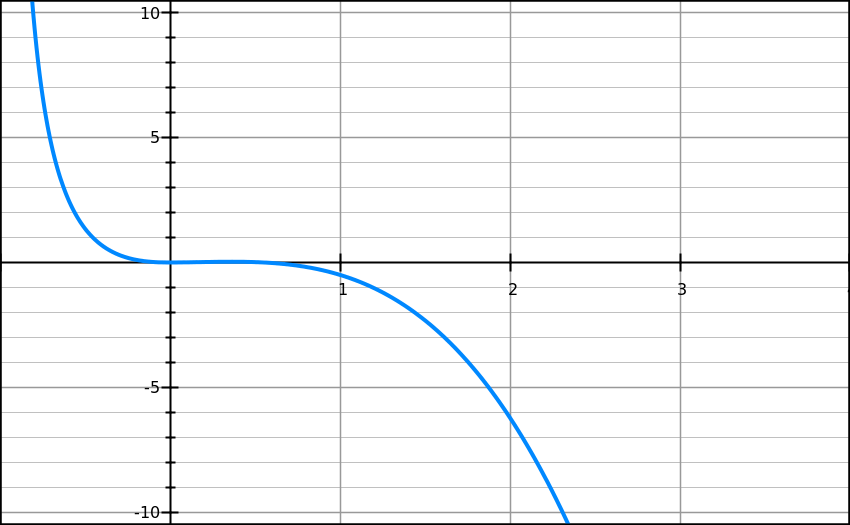
Suppose a point on the curve given above has the property that 
Based solely on the graph above, which of the following is most likely the 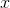
If
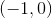

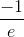

Example Question #2 : How To Describe Points By Graphing Functions
What is the critical point for 
To find the critical point, you must find the derivative first. To do that, multiply the exponent by the coefficient in front of the 




Example Question #1 : Points Of Inflection
Find the inflection point(s) of 
Inflection points can only occur when the second derivative is zero or undefined. Here we have

Therefore possible inflection points occur at 


Hence, both are inflection points
Example Question #1 : Inflection Points
Below is the graph of 


Not enough information
Possible inflection points occur when 



Example Question #1 : Points Of Inflection
Find the point(s) of inflection for the function 


There are no points of inflection.
A point of inflection is found where the graph (or image) of a function changes concavity. To find this algebraically, we want to find where the second derivative of the function changes sign, from negative to positive, or vice-versa. So, we find the second derivative of the given function 
The first derivative using the power rule



We then find where this second derivative equals 


We then look to see if the second derivative changes signs at this point. Both graphically and algebraically, we can see that the function 

Example Question #1 : Points Of Inflection
Find all the points of inflection of

There are no inflection points.
In order to find the points of inflection, we need to find 

Now we set 

To verify this is a true inflection point we need to plug in a value that is less than it and a value that is greater than it into the second derivative. If there is a sign change around the point than it is a true inflection point.
Let
Now let
Since the sign changes from a positive to a negative around the point 
Example Question #11 : Derivatives
Find all the points of inflection of
There are no points of inflection.
In order to find the points of inflection, we need to find 

Now to find the points of inflection, we need to set 

Now we can use the quadratic equation.
Recall that the quadratic equation is

where a,b,c refer to the coefficients of the equation 
In this case, a=12, b=0, c=-4.
Thus the possible points of infection are

Now to check if or which are inflection points we need to plug in a value higher and lower than each point. If there is a sign change then the point is an inflection point.
To check 

Therefore 
Now lets check 

Therefore 
Example Question #1 : Points Of Inflection
Find all the points of infection of

There are no points of inflection.
In order to find the points of inflection, we need to find 

Now lets factor 
Now to find the points of inflection, we need to set 

From this equation, we already know one of the point of inflection, 
To figure out the rest of the points of inflection we can use the quadratic equation.
Recall that the quadratic equation is


In this case, a=20, b=0, c=-18.
Thus the other 2 points of infection are
To verify that they are all inflection points we need to plug in values higher and lower than each value and see if the sign changes.
Lets plug in 
Since there is a sign change at each point, all are points of inflection.
Example Question #1 : Points Of Inflection
Find the points of inflection of

There are no points of inflection.
There are no points of inflection.
In order to find the points of inflection, we need to find
Now we set 

This last statement says that 

Example Question #1 : Points
Find the points of inflection of the following function:
The points of inflection of a given function are the values at which the second derivative of the function are equal to zero.
The first derivative of the function is


Both derivatives were found using the power rule

Solving 

To verify that this point is a true inflection point we need to plug in a value that is less than the point and one that is greater than the point into the second derivative. If there is a sign change between the two numbers than the point in question is an inflection point.
Lets plug in 

Now plug in

Therefore, 
Certified Tutor
All Calculus 1 Resources