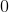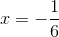If\(\displaystyle f''(x)>0\) then the graph must be concave up at the point. Based on the picture, we know that the curve is concave up on \(\displaystyle (-1,0)\) at best. The only value that falls on this interval is \(\displaystyle -e^{-1}\), which is \(\displaystyle \frac{-1}{e}\). Since \(\displaystyle e\approx2.7\), this definitely falls on the interval given and we can be sure it is concave up based on the picture.

To find the critical point, you must find the derivative first. To do that, multiply the exponent by the coefficient in front of the \(\displaystyle x\) and then subtract the exponent by \(\displaystyle 1\). Therefore, the derivative is: \(\displaystyle f{}'(x)=12x-2\). Then, to find the critical point, set the derivative equal to \(\displaystyle 0\).

\(\displaystyle 12x-2=0, x=\frac{1}{6}\).

Inflection points can only occur when the second derivative is zero or undefined. Here we have

\(\displaystyle f'(x)=4x^3-9x^2, f''(x)=12x^2-18x=6x(2x-3)\). 

Therefore possible inflection points occur at \(\displaystyle x=0\) and \(\displaystyle x=\frac{3}{2}\). However, to have an inflection point we must check that the sign of the second derivative is different on each side of the point. Here we have

\(\displaystyle f''(-1)=30, f''(1)=-6, f''(2)=12\). 

Hence, both are inflection points

Possible inflection points occur when \(\displaystyle f''(x)=0\) . This occurs at three values, \(\displaystyle x=-2, 0, 1\). However, to be an inflection point the sign of \(\displaystyle f''(x)\) must be different on either side of the critical value. Hence, only \(\displaystyle x=-2, 1\) are critical points.

A point of inflection is found where the graph (or image) of a function changes concavity. To find this algebraically, we want to find where the second derivative of the function changes sign, from negative to positive, or vice-versa. So, we find the second derivative of the given function \(\displaystyle y = x^3.\) 

The first derivative using the power rule  

\(\displaystyle y=x^n \rightarrow y'=nx^{n-1}\) is,

\(\displaystyle y' = 3x^2\) and the seconds derivative is \(\displaystyle y'' = 6x.\) 

We then find where this second derivative equals \(\displaystyle 0\).  \(\displaystyle 6x = 0\) when \(\displaystyle x = 0\).

We then look to see if the second derivative changes signs at this point. Both graphically and algebraically, we can see that the function \(\displaystyle y'' = 6x\) does indeed change sign at, and only at, \(\displaystyle x = 0\), so this is our inflection point.

In order to find the points of inflection, we need to find \(\displaystyle f''(x)\) using the power rule, \(\displaystyle f(x)=x^n \rightarrow f'(x)=nx^{n-1}\).

\(\displaystyle f(x)=-x^3+x^2-x+1\)

\(\displaystyle f'(x)=-3x^2+2x-1\)

\(\displaystyle f''(x)=-6x+2\)

Now we set \(\displaystyle f''(x)=0\), and solve for \(\displaystyle x\).

\(\displaystyle -6x+2=0\)

\(\displaystyle -6x=-2\)

\(\displaystyle x=\frac{1}{3}\)

To verify this is a true inflection point we need to plug in a value that is less than it and a value that is greater than it into the second derivative. If there is a sign change around the  point than it is a true inflection point.

Let \(\displaystyle x=0\)

\(\displaystyle f''(0)=-6(0)+2=2\)

Now let \(\displaystyle x=1\)

\(\displaystyle f''(1)=-6(1)+2=-4\)

Since the sign changes from a positive to a negative around the point \(\displaystyle x=\frac{1}{3}\), we can conclude it is an inflection point.

In order to find the points of inflection, we need to find \(\displaystyle f''(t)\) using the power rule \(\displaystyle f(x)=x^n \rightarrow f'(x)=nx^{n-1}\).

\(\displaystyle f(t)=t^4-2t^2+5t+100\)

\(\displaystyle f'(t)=4t^3-4t+5\)

\(\displaystyle f''(t)=12t^2-4\)

Now to find the points of inflection, we need to set \(\displaystyle f''(t)=0\).

\(\displaystyle 12t^2-4=0\).

Now we can use the quadratic equation.

Recall that the quadratic equation is

\(\displaystyle t=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\),

where a,b,c refer to the coefficients of the equation  \(\displaystyle at^2+bt+c=0\).

In this case, a=12, b=0, c=-4.

\(\displaystyle t=\frac{-0\pm\sqrt{0^2-4(12)(-4)}}{(2)(12)}\)

\(\displaystyle t=\frac{\pm\sqrt{192}}{24}=\frac{\pm8\sqrt{3}}{24}=\frac{\pm\sqrt{3}}{3}\)

Thus the possible points of infection are

\(\displaystyle t_1=\frac{\sqrt{3}}{3}\)

\(\displaystyle t_2=-\frac{\sqrt{3}}{3}\).

Now to check if or which are inflection points we need to plug in a value higher and lower than each point. If there is a sign change then the point is an inflection point.

To check \(\displaystyle t_1\) lets plug in \(\displaystyle x=0, x=1\).

\(\displaystyle f''(0)=12(0)^2-4=-4\)

\(\displaystyle f''(1)=12(1)^2-4=8\)

Therefore \(\displaystyle t_1\) is an inflection point. 

Now lets check \(\displaystyle t_2\) with \(\displaystyle x=0, x=-1\).

\(\displaystyle f''(0)=12(0)^2-4=-4\)

\(\displaystyle f''(-1)=12(-1)^2-4=8\)

Therefore \(\displaystyle t_2\) is also an inflection point. 

In order to find the points of inflection, we need to find \(\displaystyle f''(t)\) using the power rule \(\displaystyle f(x)=x^n \rightarrow f'(x)=nx^{n-1}\).

\(\displaystyle f(t)=t^5-3t^3+2t+100\)

\(\displaystyle f'(t)=5t^4-9t^2+2\)

\(\displaystyle f''(t)=20t^3-18t\)

Now lets factor \(\displaystyle f''(t)\).

\(\displaystyle f''(t)=t(20t^2-18)\)

Now to find the points of inflection, we need to set \(\displaystyle f''(t)=0\).

\(\displaystyle t(20t^2-18)=0\).

From this equation, we already know one of the point of inflection, \(\displaystyle t_1=0\).

To figure out the rest of the points of inflection we can use the quadratic equation.

Recall that the quadratic equation is

\(\displaystyle t=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\), where a,b,c refer to the coefficients of the equation

\(\displaystyle at^2+bt+c=0\).

In this case, a=20, b=0, c=-18.

\(\displaystyle t=\frac{-0\pm\sqrt{0^2-4(20)(-18)}}{(2)(20)}\)

\(\displaystyle t=\frac{\pm\sqrt{1440}}{40}=\frac{\pm12\sqrt{10}}{40}=\frac{\pm3\sqrt{10}}{10}\)

Thus the other 2 points of infection are

\(\displaystyle t_2=\frac{3\sqrt{10}}{10}\)

\(\displaystyle t_3=-\frac{3\sqrt{10}}{10}\)

To verify that they are all inflection points we need to plug in values higher and lower than each value and see if the sign changes.

Lets plug in \(\displaystyle x=-1, x=-\frac{1}{2}, x=\frac{1}{2}, x=1\) 

\(\displaystyle f''(-1)=20(-1)^3-18(-1)=-2\)

\(\displaystyle f''\left(-\frac{1}{2}\right)=20\left(-\frac{1}{2} \right )^3-18\left(-\frac{1}{2} \right )=6.5\)

\(\displaystyle f''\left(\frac{1}{2}\right)=20\left(\frac{1}{2} \right )^3-18\left(\frac{1}{2} \right )=-6.5\)

\(\displaystyle f''(1)=20(1)^3-18(1)=2\)

Since there is a sign change at each point, all are points of inflection.

In order to find the points of inflection, we need to find \(\displaystyle f''(x)\)

\(\displaystyle f(x)=x^2-2x+1\)

\(\displaystyle f'(x)=2x-2\)

\(\displaystyle f''(x)=2\)

Now we set \(\displaystyle f''(x)=0\).

\(\displaystyle 0=2\).

This last statement says that \(\displaystyle f''(x)\) will never be \(\displaystyle 0\). Thus there are no points of inflection.

The points of inflection of a given function are the values at which the second derivative of the function are equal to zero.

The first derivative of the function is 

\(\displaystyle f{}'(x)=3x^2+4x+1\), and the derivative of this function (the second derivative of the original function), is 

\(\displaystyle f''(x)=6x+4\).

Both derivatives were found using the power rule 

\(\displaystyle \frac{d}{dx}x^n=nx^{n-1}\). 

Solving \(\displaystyle 0=6x+4\), \(\displaystyle x=-\frac{2}{3}\).

To verify that this point is a true inflection point we need to plug in a value that is less than the point and one that is greater than the point into the second derivative. If there is a sign change between the two numbers than the point in question is an inflection point.

Lets plug in \(\displaystyle {}x=-1\), 

\(\displaystyle 6(-1)+4=-2\).

Now plug in \(\displaystyle {}x=0\)

\(\displaystyle 6(0)+4=4\).

Therefore, \(\displaystyle x=-\frac{2}{3}\) is the only point of inflection of the function.