Create an account to track your scores
and create your own practice tests:
All Calculus AB Resources
Want to review Calculus AB but don’t feel like sitting for a whole test at the moment? Varsity Tutors has you covered with thousands of different Calculus AB flashcards! Our Calculus AB flashcards allow you to practice with as few or as many questions as you like. Get some studying in now with our numerous Calculus AB flashcards.
Suzanne M
Certified Tutor
Certified Tutor
New Mexico State University-Main Campus, Bachelor of Education, Elementary School Teaching. University of New Mexico-Main Cam...
Popular Subjects
Statistics Tutors in Houston, SAT Tutors in Philadelphia, ACT Tutors in Washington DC, Math Tutors in Houston, Spanish Tutors in Los Angeles, Spanish Tutors in Seattle, LSAT Tutors in Miami, SSAT Tutors in Miami, ISEE Tutors in Boston, SSAT Tutors in Los Angeles
Popular Courses & Classes
ISEE Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Boston, MCAT Courses & Classes in Miami, GMAT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Seattle, SAT Courses & Classes in Boston, MCAT Courses & Classes in Seattle, GRE Courses & Classes in Chicago, Spanish Courses & Classes in Denver
Popular Test Prep
MCAT Test Prep in Miami, GRE Test Prep in Los Angeles, GRE Test Prep in San Francisco-Bay Area, SAT Test Prep in Seattle, ACT Test Prep in Seattle, GMAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Boston, MCAT Test Prep in Boston, MCAT Test Prep in New York City, SSAT Test Prep in Washington DC


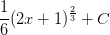

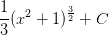



 , happens to be one order higher than the factor outside the radical,
, happens to be one order higher than the factor outside the radical,  You know that if you take a derivative of a second order polynomial you will get a first order polynomial, so let's define the variable:
You know that if you take a derivative of a second order polynomial you will get a first order polynomial, so let's define the variable:  (1)
(1) to write the differential for
to write the differential for  ,
,  (2)
(2) , to obtain
, to obtain  . Now if we look at the original integral we can rewrite in terms of
. Now if we look at the original integral we can rewrite in terms of 

 .
. 
![= \frac{1}{2}\left[\frac{1}{\frac{1}{2}+1}u^{\frac{1}{2}+1} \right ]+C](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/741662/gif.latex)



 using equation (1), we conclude,
using equation (1), we conclude, 













