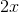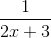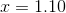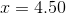We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

College Algebra : Exponential Functions

Study concepts, example questions & explanations for College Algebra

Create An Account

All College Algebra Resources

5 Diagnostic Tests 84 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : College Algebra

Solve: e^l^n^(^2^x^+^3^)

Possible Answers:

$\frac{1}{2x+3}$

2x+3

The answer does not exist.

Correct answer:

2x+3

Explanation:

To solve e^l^n^(^2^x^+^3^) , it is necessary to know the property of .

e^l^n^(^x^)=x

Since and the terms cancel due to inverse operations, the answer is what's left of the term.

The answer is: 2x+3

Report an Error

Example Question #2 : College Algebra

Which equation is equivalent to:

$\log _{4}\left( \frac{1}{2}\right)=x$

Possible Answers:

$\frac{1^{4}}{2}=x^{4}$

$(4)^{x}=\left(\frac{1}{2}\right)^{x}$

$4^{\frac{1}{2}}=x$

$\left(\frac{1}{2}\right)^{4}=x$

$4^{x}=\frac{1}{2}$

Correct answer:

$4^{x}=\frac{1}{2}$

Explanation:

$log{_{a}}^{b}=x$ , b>0

$\Rightarrow a^{x}=b$

So, ${{log_{4}}^{\frac{1}{2}}}=x\Rightarrow 4^{x}=\frac{1}{2}$

Report an Error

Example Question #3 : College Algebra

$Log_{b}x=y$

What is the inverse of the log function?

Possible Answers:

$b^{x}=y$

$x^{b}=y$

$b^{y}=x$

$y^{b}=x$

$b=x\cdot y$

Correct answer:

$b^{y}=x$

Explanation:

This is a general formula that you should memorize. The inverse of $Log_{b}x=y$ is $b^{y}=x$ . You can use this formula to change an equation from a log function to an exponential function.

Report an Error

Example Question #1 : Exponential Functions

Rewrite the following expression as an exponential expression:

log_3b=14,000

Possible Answers:

$b^{14,000}=3$

$3^{14,000}=b$

14,000^3=b

b^3=14,000

Correct answer:

$3^{14,000}=b$

Explanation:

Rewrite the following expression as an exponential expression:

log_3b=14,000

Recall the following property of logs and exponents:

log_b(a)=c

Can be rewritten in the following form:

b^c=a

So, taking the log we are given;

log_3b=14,000

We can rewrite it in the form:

$3^{14,000}=b$

So b must be a really huge number!

Report an Error

Example Question #2 : Exponential Functions

Convert the following logarithmic equation to an exponential equation:

$log_{13}b=147$

Possible Answers:

147^b=13

$13^{147}=b$

$13^{b}=147$

$b^{13}=147$

Correct answer:

$13^{147}=b$

Explanation:

Convert the following logarithmic equation to an exponential equation:

$log_{13}b=147$

Recall the following:

This

log_b(a)=c

Can be rewritten as

b^c=a

So, our given logarithm

$log_{13}b=147$

Can be rewritten as

$13^{147}=b$

Fortunately we don't need to expand, because this woud be a very large number!

Report an Error

Example Question #6 : College Algebra

Convert the following logarithmic equation to an exponential equation.

log_3(14x)=156

Possible Answers:

$3^{14x}=156$

$3^{156}=14x$

156=(14x)^3

$(14x)^{156}=3$

Correct answer:

$3^{156}=14x$

Explanation:

Convert the following logarithmic equation to an exponential equation.

log_3(14x)=156

To convert from logarithms to exponents, recall the following property:

log_b(x)=a

Can be rewritten as:

b^a=x

So, starting with

log_3(14x)=156 ,

We can get

$3^{156}=14x$

Report an Error

Example Question #7 : College Algebra

Solve the following:

5^x=125

Possible Answers:

625

Correct answer:

Explanation:

To solve the following, you must "undo" the 5 with taking log based 5 of both sides. Thus,

5^x=125

$\log_5{5^x}=\log_5{125}$

$x=\log_5{125}$

The right hand side can be simplified further, as 125 is a power of 5. Thus,

$x=\log_5{125}$

$x=\log_5{5^3}$

x=3

Report an Error

Example Question #8 : College Algebra

Solve for :

$2^{x}+ 2 ^{x+2} = 171$

(Nearest hundredth)

Possible Answers:

The equation has no solution.

$x \approx 3.65$

$x \approx 2.84$

$x \approx 2.71$

$x \approx 5.10$

Correct answer:

$x \approx 5.10$

Explanation:

Apply the Product of Powers Property to rewrite the second expression:

$2^{x}+ 2 ^{x+2} = 171$

$2^{x}+ 2 ^{2} \cdot 2 ^{x} = 171$

$1 \cdot 2^{x}+ 4 \cdot 2 ^{x} = 171$

Distribute out:

$(1 + 4) \cdot 2 ^{x} = 171$

$5 \cdot 2 ^{x} = 171$

Divide both sides by 5:

$\frac{5 \cdot 2 ^{x}}{5} = \frac{171}{5}$

$2 ^{x} = 34.2$

Take the natural logarithm of both sides (and note that you can use common logarithms as well):

$\ln 2 ^{x} = \ln 34.2$

Apply a property of logarithms:

$x \ln 2 = \ln 34.2$

Divide by $\ln 2$ and evaluate:

$\frac{x \ln 2}{\ln2} = \frac{\ln 34.2}{\ln2}$

$x = \frac{3.5322 }{0.6931 }$

$x \approx 5.10$

Report an Error

Example Question #3 : Exponential And Logarithmic Functions

Solve for :

$3^{2x+ 1} = 9^{2x- 4 }$

(Nearest hundredth, if applicable).

Possible Answers:

x = 4.50

x= 3.25

x = 3.40

The equation has no solution.

x= 1.10

Correct answer:

x = 4.50

Explanation:

$9 = 3^{2}$ , so rewrite the expression at right as a power of 3 using the Power of a Power Property:

$3^{2x+ 1} = 9^{2x- 4 }$

$3^{2x+ 1} = (3^{2} )^{2x- 4 }$

$3^{2x+ 1} = 3^{2(2x- 4 )}$

Set the exponents equal to each other and solve the resulting linear equation:

2x+ 1 = 2(2x-4)

Distribute:

2x+ 1 = 4x-8

Subtract and 1 from both sides; we can do this simultaneously:

2x+ 1 - 4x - 1 = 4x-8 - 4x - 1

- 2x = -9

Divide by :

$\frac{- 2x}{-2} = \frac{-9}{-2}$

x =4.5

Report an Error

View College Algebra Tutors

Justin
Certified Tutor

Vanderbilt University, Bachelor, Computer Science, Mathematics, & Philosophy.

View College Algebra Tutors

John
Certified Tutor

Arizona State University, Bachelor of Science, Microbiology.

View College Algebra Tutors

Mehak
Certified Tutor

Guru Nanak Dev University, Bachelor of Science, Chemistry. Guru Nanak Dev University, Master of Science, Chemistry.

All College Algebra Resources

5 Diagnostic Tests 84 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Chicago, SSAT Tutors in Denver, SAT Tutors in San Francisco-Bay Area, Physics Tutors in Atlanta, GRE Tutors in Boston, Computer Science Tutors in Philadelphia, Spanish Tutors in San Diego, Chemistry Tutors in San Francisco-Bay Area, SAT Tutors in Atlanta, SAT Tutors in San Diego

Popular Courses & Classes

LSAT Courses & Classes in Atlanta, ISEE Courses & Classes in New York City, SAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Washington DC, LSAT Courses & Classes in Seattle, SSAT Courses & Classes in Chicago, GMAT Courses & Classes in Houston, ISEE Courses & Classes in Denver, SSAT Courses & Classes in Washington DC, ACT Courses & Classes in Washington DC

Popular Test Prep

LSAT Test Prep in Houston, ISEE Test Prep in Los Angeles, ISEE Test Prep in San Francisco-Bay Area, SAT Test Prep in Dallas Fort Worth, GRE Test Prep in Phoenix, SSAT Test Prep in Los Angeles, ISEE Test Prep in New York City, ACT Test Prep in Washington DC, GMAT Test Prep in Los Angeles, MCAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

College Algebra : Exponential Functions

Study concepts, example questions & explanations for College Algebra

All College Algebra Resources

Example Questions

Example Question #1 : College Algebra

Example Question #2 : College Algebra

Example Question #3 : College Algebra

Example Question #1 : Exponential Functions

Example Question #2 : Exponential Functions

Example Question #6 : College Algebra

Example Question #7 : College Algebra

Example Question #8 : College Algebra

Example Question #3 : Exponential And Logarithmic Functions

All College Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: