All College Algebra Resources
Example Questions
Example Question #1 : Logarithmic Functions
Solve the following for x:
To solve, you must first "undo" the log. Since no base is specified, you assume it is 10. Thus, we need to take 10 to both sides.
Now, simply solve for x.
Example Question #11 : College Algebra
Simplify the following:
To solve, you must combine the logs into 1 log, instead of three separate ones. To do this, you must remember that when adding logs, you multiply their insides, and when you subtract them, you add their insides. Therefore,
Example Question #11 : College Algebra
Solve for y in the following expression:
To solve for y we first need to get rid of the logs.
Then we get 
After that, we simply have to divide by 5x on both sides:
Example Question #13 : College Algebra
Solve for 
To solve this natural logarithm equation, we must eliminate the 




This simplifies to

Continuing to solve for x,
Example Question #4 : Logarithmic Functions
Solve for 
To eliminate the 


This simplifies to
Example Question #12 : College Algebra

True or false:
if and only if either 

False
True
False
is a direct statement of the Change of Base Property of Logarithms. If 



Example Question #13 : College Algebra
Evaluate



Example Question #7 : Logarithmic Functions
Use the properties of logarithms to rewrite as a single logarithmic expression:



Example Question #8 : Logarithmic Functions
Use the properties of logarithms to rewrite as a single logarithmic expression:
None of the other choices gives the correct response.


By the Change of Base Property,


the correct response.
Example Question #9 : Logarithmic Functions
Expand the logarithm:
None of these
We expand this logarithm based on the property:
and 
All College Algebra Resources


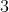






































































![\ln \sqrt[3]{\frac{x}{y}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1036013/gif.latex)





![\ln \sqrt[3]{\frac{x}{y}}\rightarrow\frac{1}{3}\ln\frac{x}{y}\rightarrow \boldsymbol{\frac{1}{3}(\ln x-\ln y)}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1036016/gif.latex)



