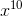Call Now to Set Up Tutoring:

(888) 888-0446

College Algebra : Review and Other Topics

Study concepts, example questions & explanations for College Algebra

Create An Account

All College Algebra Resources

5 Diagnostic Tests 84 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Simplifying Exponents

Simplify the expression:

$(3x^4y^2)(4xy^2)^{-3}$ $\displaystyle (3x^4y^2)(4xy^2)^{-3}$

Possible Answers:

$\displaystyle 3xy$

Cannot be simplified

$\frac{3x}{64y^4}$ $\displaystyle \frac{3x}{64y^4}$

$\frac{3x}{64y^3}$ $\displaystyle \frac{3x}{64y^3}$

$\frac{3x}{16y^3}$ $\displaystyle \frac{3x}{16y^3}$

Correct answer:

$\frac{3x}{64y^4}$ $\displaystyle \frac{3x}{64y^4}$

Explanation:

Begin by distributing the exponent through the parentheses. The power rule dictates that an exponent raised to another exponent means that the two exponents are multiplied:

$(3x^{4}y^2)(4xy^2)^{-3}= (3xy^2)(4^{-3}x^{-3}y^{-6})$ $\displaystyle (3x^{4}y^2)(4xy^2)^{-3}= (3xy^2)(4^{-3}x^{-3}y^{-6})$

Any negative exponents can be converted to positive exponents in the denominator of a fraction:

$\frac{3x^4y^2}{64x^3y^6}$ $\displaystyle \frac{3x^4y^2}{64x^3y^6}$

The like terms can be simplified by subtracting the power of the denominator from the power of the numerator:

$\frac{3x^4y^2}{64x^3y^6}=\frac{3}{64}x^{4-3}y^{2-6}=\frac{3}{64}xy^{-4}$ $\displaystyle \frac{3x^4y^2}{64x^3y^6}=\frac{3}{64}x^{4-3}y^{2-6}=\frac{3}{64}xy^{-4}$

$\frac{3x}{64y^4}$ $\displaystyle \frac{3x}{64y^4}$

Report an Error

Example Question #1 : Expressions & Equations

Simplify:

$\displaystyle (4x^3)^4$

Possible Answers:

16x^7 $\displaystyle 16x^7$

512x $\displaystyle 512x$

$256x^{12}$ $\displaystyle 256x^{12}$

4x^7 $\displaystyle 4x^7$

$4x^{12}$ $\displaystyle 4x^{12}$

Correct answer:

$256x^{12}$ $\displaystyle 256x^{12}$

Explanation:

Use the power rule to distribute the exponent:

$(4x^3)^4\rightarrow 4^4\cdot x^{3\cdot 4}\rightarrow 256x^{12}$ $\displaystyle (4x^3)^4\rightarrow 4^4\cdot x^{3\cdot 4}\rightarrow 256x^{12}$

Report an Error

Example Question #1 : Integer Exponents

Simplify the following expression:

$\displaystyle (9x^6y^2z^5)^2$

Possible Answers:

$81x^{12}y^4z^{10}$ $\displaystyle 81x^{12}y^4z^{10}$

$11x^{12}y^4z^{10}$ $\displaystyle 11x^{12}y^4z^{10}$

$81x^{8}y^4z^{7}$ $\displaystyle 81x^{8}y^4z^{7}$

$18x^{12}y^4z^{10}$ $\displaystyle 18x^{12}y^4z^{10}$

Correct answer:

$81x^{12}y^4z^{10}$ $\displaystyle 81x^{12}y^4z^{10}$

Explanation:

Simplify the following expression:

$\displaystyle (9x^6y^2z^5)^2$

To raise exponents to another power, we need to multiply them:

$(9x^6y^2z^5)^2=9^2x^{6*2}y^{2*2}z^{5*2}=81x^{12}y^4z^{10}$ $\displaystyle (9x^6y^2z^5)^2=9^2x^{6*2}y^{2*2}z^{5*2}=81x^{12}y^4z^{10}$

So we get:

$81x^{12}y^4z^{10}$ $\displaystyle 81x^{12}y^4z^{10}$

Report an Error

Example Question #2 : Integer Exponents

Simplify.

$(x^4)^{6}$ $\displaystyle (x^4)^{6}$

Possible Answers:

$x^{46}$ $\displaystyle x^{46}$

$x^{24}$ $\displaystyle x^{24}$

$x^{-2}$ $\displaystyle x^{-2}$

$x^{10}$ $\displaystyle x^{10}$

x^2 $\displaystyle x^2$

Correct answer:

$x^{24}$ $\displaystyle x^{24}$

Explanation:

When an exponent is being raised by another exponent, we just multiply the powers of the exponents and keep the base the same.

$(x^4)^{6}=x^{4*6}=x^{24}$ $\displaystyle (x^4)^{6}=x^{4*6}=x^{24}$

Report an Error

Example Question #21 : Distributing Exponents (Power Rule)

Simplify.

$(\frac{x^5}{y^3})^3$ $\displaystyle (\frac{x^5}{y^3})^3$

Possible Answers:

$\frac{x^{8}}{y^6}$ $\displaystyle \frac{x^{8}}{y^6}$

$\frac{x^{15}}{y^8}$ $\displaystyle \frac{x^{15}}{y^8}$

$\frac{x^{15}}{y^{13}}$ $\displaystyle \frac{x^{15}}{y^{13}}$

$\frac{x^{15}}{y^9}$ $\displaystyle \frac{x^{15}}{y^9}$

$\frac{x^{15}}{y^3}$ $\displaystyle \frac{x^{15}}{y^3}$

Correct answer:

$\frac{x^{15}}{y^9}$ $\displaystyle \frac{x^{15}}{y^9}$

Explanation:

When an exponent is being raised by another exponent, we just multiply the powers of the exponents and keep the base the same.

$(\frac{x^5}{y^3})^{3}=\frac{x^{5*3}}{y^{3*3}}=\frac{x^{15}}{y^{9}}$ $\displaystyle (\frac{x^5}{y^3})^{3}=\frac{x^{5*3}}{y^{3*3}}=\frac{x^{15}}{y^{9}}$

Report an Error

Example Question #4 : Review And Other Topics

Combine the following terms:

$\displaystyle 5x^4*3t^3*8x^3$

Possible Answers:

$\displaystyle 120x^7t^3$

$120x^{36}$ $\displaystyle 120x^{36}$

$\displaystyle 16x^7t^3$

$120x^{10}$ $\displaystyle 120x^{10}$

Correct answer:

$\displaystyle 120x^7t^3$

Explanation:

Combine the following terms:

$\displaystyle 5x^4*3t^3*8x^3$

We need to multiply three terms together. We should recognize that the t must be left alone, because it cannot be combined with the x's.

First, multiply all three coefficients

$\displaystyle 5*3*8=120$

Next, combine the x's. Because we are multiplying, we will add the exponents.

$\displaystyle x^4*x^3=x^7$

Now, put it all together to get:

$\displaystyle 120x^7t^3$

Report an Error

Example Question #2 : Integer Exponents

Evaluate

X^7/X^4 $\displaystyle X^7/X^4$

Possible Answers:

$X^{28}$ $\displaystyle X^{28}$

$X^{7/4}$ $\displaystyle X^{7/4}$

$X^{-3}$ $\displaystyle X^{-3}$

7/4X $\displaystyle 7/4X$

X^3 $\displaystyle X^3$

Correct answer:

X^3 $\displaystyle X^3$

Explanation:

When common variables with exponents are divided, the exponents are subtracted.

$X^7/X^4 = X^{7-4} = X^3$ $\displaystyle X^7/X^4 = X^{7-4} = X^3$

Report an Error

Example Question #3 : Integer Exponents

Evaluate

X^8*X^6 $\displaystyle X^8*X^6$

Possible Answers:

$X^{48}$ $\displaystyle X^{48}$

14X $\displaystyle 14X$

$X^{14}$ $\displaystyle X^{14}$

48X $\displaystyle 48X$

$X^{2}$ $\displaystyle X^{2}$

Correct answer:

$X^{14}$ $\displaystyle X^{14}$

Explanation:

When like terms with exponents are multiplied, you add the exponents.

$X^8*X^6 = X^{8+6} = X^{14}$ $\displaystyle X^8*X^6 = X^{8+6} = X^{14}$

Report an Error

Example Question #4 : Integer Exponents

Evaluate the following:

$x^{2}*x^{4}=$ $\displaystyle x^{2}*x^{4}=$

Possible Answers:

$2x^{4}$ $\displaystyle 2x^{4}$

$\displaystyle 4x$

$x^{2}$ $\displaystyle x^{2}$

$x^{8}$ $\displaystyle x^{8}$

$x^{6}$ $\displaystyle x^{6}$

Correct answer:

$x^{6}$ $\displaystyle x^{6}$

Explanation:

When similar terms raised to n are multiplied, simply add the exponents. Thus

$x^{2}*x^{4}=x^{2+4}=x^{6}$ $\displaystyle x^{2}*x^{4}=x^{2+4}=x^{6}$

Report an Error

Example Question #5 : Integer Exponents

$x^{3}*x^{5}=$ $\displaystyle x^{3}*x^{5}=$

Possible Answers:

$x^{2}$ $\displaystyle x^{2}$

$x^{5}$ $\displaystyle x^{5}$

$x^{15}$ $\displaystyle x^{15}$

15x $\displaystyle 15x$

$x^{8}$ $\displaystyle x^{8}$

Correct answer:

$x^{8}$ $\displaystyle x^{8}$

Explanation:

When similar terms raised to n are multiplied, simply add the exponents. Thus

$x^{3}*x^{5}=x^{3+5}=x^{8}$ $\displaystyle x^{3}*x^{5}=x^{3+5}=x^{8}$

Report an Error

View College Algebra Tutors

Jesse
Certified Tutor

Central Washington University, Bachelor in Arts, Biology, General.

View College Algebra Tutors

Kendall
Certified Tutor

Relay Graduate School of Education, Master of Arts Teaching, Education.

View College Algebra Tutors

Shakeel
Certified Tutor

All College Algebra Resources

5 Diagnostic Tests 84 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in New York City, French Tutors in Los Angeles, GMAT Tutors in Philadelphia, GRE Tutors in Houston, LSAT Tutors in Chicago, SAT Tutors in Denver, Reading Tutors in San Francisco-Bay Area, ACT Tutors in Houston, Algebra Tutors in Phoenix, Physics Tutors in Boston

Popular Courses & Classes

GMAT Courses & Classes in Miami, GRE Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Houston, ACT Courses & Classes in Houston, Spanish Courses & Classes in Phoenix, LSAT Courses & Classes in Washington DC, MCAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Atlanta, MCAT Courses & Classes in Denver, SSAT Courses & Classes in Washington DC

Popular Test Prep

SSAT Test Prep in Philadelphia, SAT Test Prep in Miami, GMAT Test Prep in Washington DC, GMAT Test Prep in Los Angeles, ACT Test Prep in Houston, ISEE Test Prep in Houston, ACT Test Prep in San Francisco-Bay Area, GMAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Atlanta, SSAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

College Algebra : Review and Other Topics

Study concepts, example questions & explanations for College Algebra

All College Algebra Resources

Example Questions

Example Question #1 : Simplifying Exponents

Example Question #1 : Expressions & Equations

Example Question #1 : Integer Exponents

Example Question #2 : Integer Exponents

Example Question #21 : Distributing Exponents (Power Rule)

Example Question #4 : Review And Other Topics

Example Question #2 : Integer Exponents

Example Question #3 : Integer Exponents

Example Question #4 : Integer Exponents

Example Question #5 : Integer Exponents

All College Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: